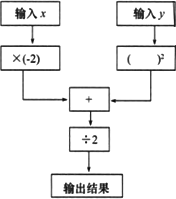
题目内容
| |||||
答案:
解析:
解析:
|
解:(1)MN=MC+CN= (2)MN= (3)如图所示:
因为M、N分别为AC、BC的中点,所以AM=MC= 结论:A、B、C三点的顺序无论怎样变化,M、N分别为AC、BC的中点时,MN的长度总是线段AB长度的一半. |

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目