Question

（2008•朝阳区二模）如图，△AOC在平面直角坐标系中，∠AOC=90°，且O为坐标原点，点A、C分别在坐标轴上，AO=4，OC=3，将△AOC绕点C按逆时针方向旋转，旋转后的三角形记为△CA′O′．
（1）当CA边落在y轴上（其中旋转角为锐角）时，一条抛物线经过A、C两点且与直线AA′相交于x轴下方一点D，如果S_△AOD=9，求这条抛物线的解析式；
（2）继续旋转△CA′O′，当以CA′为直径的⊙P与（1）中抛物线的对称轴相切时，圆心P是否在抛物线上，请说明理由．

Answer 1

分析：（1）根据已知条件先求出直线AA′的解析式，再求出D点的坐标，即可求出抛物线的解析式；
（2）由y=-

1

4

x2-

1

4

x+3得对称轴为x=-

1

2

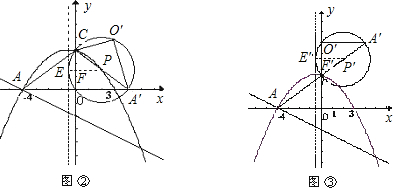
．由⊙P与抛物线的对称轴相切，可有两种情况：情况1：如图②，过点P向抛物线的对称轴作垂线，交对称轴于点E，交y轴于点F，点P到对称轴的距离PE等于⊙P的半径，求出点P的坐标即可判断；情况2：如图③，过点P′向抛物线的对称轴作垂线，交对称轴于点E′，交轴于点F′，求出点P′的坐标即可证明；

解答：解：（1）在Rt△AOC中，∵AO=4，OC=3，∴AC=5．
由旋转可知A′C=AC=5．
∴A′O=A′C-OC=2．
∴A（-4，0），C（0，3），A′（0，-2）．
可求得直线AA′的解析式为y=-

1

2

x-2．
抛物线与直线AA′交于点D，设点D（x，y），
∵S_△AOD=9，
∴

1

2

OA•(-y)=9．解得y=-

9

2

．
将y=-

9

2

代入y=-

1

2

x-2，得x=5．
∴D（5，-

9

2

）．
∵抛物线过A、C、D三点，
∴可求得抛物线的解析式为y=-

1

4

x2-

1

4

x+3；

（2）由y=-

1

4

x2-

1

4

x+3得对称轴为x=-

1

2

．
∵⊙P与抛物线的对称轴相切，可有两种情况：
情况1：如图②，过点P向抛物线的对称轴作垂线，交对称轴于点E，交y轴于点F，点P到对称轴的距离PE等于⊙P的半径，
即PE=

5

2

，PF=2．CF=

PC2-PF2

 =

3

2

．
∴FO=CO-CF=

3

2

．
∴P（2，

3

2

）．
∵点P的坐标满足y=-

1

4

x2-

1

4

x+3，
∴点P在抛物线上．

情况2：如图③，过点P′向抛物线的对称轴作垂线，交对称轴于点E′，交轴于点F'．
同理可求得点P′(2，

9

2

)．
∵点P'坐标不满足抛物线y=-

1

4

x2-

1

4

x+3，
∴此点P′不在抛物线上．

点评：本题考查了二次函数综合题，难度较大，关键是注意由⊙P与抛物线的对称轴相切，可有两种情况，需要分情况讨论．