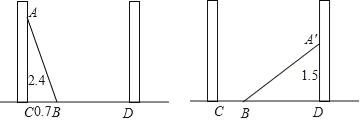
题目内容
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB= ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 . 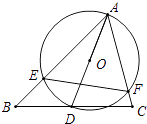
【答案】![]()
【解析】解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
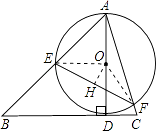
在Rt△ADB中,∠ABC=45°,AB= ![]() ,
,
∴AD=BD=1,即此时圆的直径为1,
∵∠EOF=2∠BAC=120°,
而∠EOH=∠HOF,
∴∠EOH=60°,
在Rt△EOH中,EH=OEsin∠EOH= ![]() sin60°=
sin60°= ![]() ,
,
∵OH⊥EF,
∴EH=FH,
∴EF=2EH= ![]() ,
,
即线段EF长度的最小值为 ![]() .
.
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解垂线段最短的相关知识,掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用,以及对垂径定理的推论的理解,了解推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某童装店有A、B两种型号的童装,其进价与售价如下表所示:
型号 | 进价(元) | 售价(元) |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要,服装店决定:购进A种服装的数量要比购进B种服装的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总利润不少于699元.若假设购进B种服装x件,那么:
(1)请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示;
(2)请问该服装店有几种满足条件的进货方案?哪种方案获利最多?