题目内容
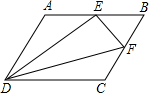 已知?ABCD中,若△ADE、△BEF、△CDF的面积分别为5、3、4,求△DEF的面积.
已知?ABCD中,若△ADE、△BEF、△CDF的面积分别为5、3、4,求△DEF的面积.
分析:过A作AH⊥CD,垂足为H,设AH=x,过F作FM⊥CD,垂足为M,MF的延长线交AB于N,设FM=h,(x>h),根据△ADE、△BEF的面积公式用x、h分别表示AE、BE,根据CD=AB=AE+BE表示CD,再根据S△CFD=CD×
=4,列方程求x、h的关系,求?ABCD的面积,用作差法求△DEF的面积.
| h |
| 2 |
解答: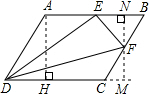 解:过A作AH⊥CD,垂足为H,设AH=x,过F作FM⊥CD,垂足为M,MF的延长线交AB于N,设FM=h,(x>h),
解:过A作AH⊥CD,垂足为H,设AH=x,过F作FM⊥CD,垂足为M,MF的延长线交AB于N,设FM=h,(x>h),
依题意应有:S△DAE=AE×
=5,
解得AE=
,
S△EBF=EB×
=3,
解得BE=
,
∵S△CFD=CD×
=4,CD=AB=AE+BE=
+
,
∴(
+
)×
=4,
整理,得4x2-12xh+5h2=0,
即(2x-h)(2x-5h)=0,
∵x>h,
∴2x=h(舍去),2x=5h,
∴CD=
+
=
,
∴S平行四边形ABCD=x•CD=x×
,
=
×
,
=20,
∴S△DEF=S平行四边形ABCD-S△DAE-S△EBF-S△DCF,
=20-5-3-4,
=8.
 解:过A作AH⊥CD,垂足为H,设AH=x,过F作FM⊥CD,垂足为M,MF的延长线交AB于N,设FM=h,(x>h),
解:过A作AH⊥CD,垂足为H,设AH=x,过F作FM⊥CD,垂足为M,MF的延长线交AB于N,设FM=h,(x>h),依题意应有:S△DAE=AE×
| x |
| 2 |
解得AE=
| 10 |
| x |
S△EBF=EB×
| x-h |
| 2 |
解得BE=
| 6 |
| x-h |
∵S△CFD=CD×
| h |
| 2 |
| 10 |
| x |
| 6 |
| x-h |
∴(
| 10 |
| x |
| 6 |
| x-h |
| h |
| 2 |
整理,得4x2-12xh+5h2=0,
即(2x-h)(2x-5h)=0,
∵x>h,
∴2x=h(舍去),2x=5h,
∴CD=
| 10 |
| x |
| 6 |
| x-h |
| 8 |
| h |
∴S平行四边形ABCD=x•CD=x×
| 8 |
| h |
=
| 5h |
| 2 |
| 8 |
| h |
=20,
∴S△DEF=S平行四边形ABCD-S△DAE-S△EBF-S△DCF,
=20-5-3-4,
=8.
点评:本题考查了三角形面积的表示方法.关键是构造每个三角形的高,用已知面积表示底,根据平行四边形的性质将底过渡.

练习册系列答案
相关题目
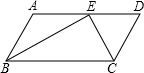 已知?ABCD中,BE平分∠ABC交AD于E,若CE平分∠DCB,且AB=2,求:?ABCD的其余边长.
已知?ABCD中,BE平分∠ABC交AD于E,若CE平分∠DCB,且AB=2,求:?ABCD的其余边长. 如图,已知?ABCD中,AE⊥BC于E,AF⊥CD于F.若?ABCD的周长为36cm,AE=4cm,AF=5cm,则AD=
如图,已知?ABCD中,AE⊥BC于E,AF⊥CD于F.若?ABCD的周长为36cm,AE=4cm,AF=5cm,则AD= 如图已知?ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F
如图已知?ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F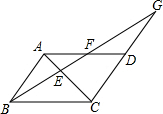 如图,已知?ABCD中,过点B的直线与AC相交于点E、与AD相交于点F、与CD的延长线相交于点G,若BE=5,EF=2,则FG=
如图,已知?ABCD中,过点B的直线与AC相交于点E、与AD相交于点F、与CD的延长线相交于点G,若BE=5,EF=2,则FG=