题目内容
(2008•防城港)“假日旅乐园”中一种新型水上滑梯如图,其中线段PA表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道AB可以看作反比例函数图象的一部分,滑道BCD可以看作是二次函数图象的一部分,两滑道的连接点B为抛物线BCD的顶点,且点B到水面的距离BE=2m,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离CG= m,与点B的水平距离CF=2m.
m,与点B的水平距离CF=2m.(1)求反比例函数的解析式及其自变量的取值范围.
(2)求二次函数的解析式及其自变量的取值范围.
(3)小明从点B滑水面上点D处时,试求他所滑过的水平距离d.

【答案】分析:(1)在题中,BE=2,B到y轴的距离是5,即反比例函数图象上一点的横坐标和纵坐标都已告知,则可求出比例系数k;
(2)由(1)知,抛物线顶点坐标已知,可列两个关系式,又C点坐标已知则可列一个关于a、b、c的方程组,进而求出解析式.
解答:解:(1)∵BE=2,B到y轴的距离是5,
∴B点坐标为(5,2),
若设反比例解析式为y=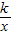 ,
,
则k=10,
∴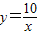 ,
,
当y=5时,x=2即A点之比为(2,5),
∴2≤x≤5;
(2)设二次函数解析式为y=ax2+bx+c,
由题意可知,顶点坐标为(5,2),C点坐标为(7, ),
),
∴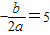 ,
,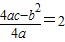 ,
,
?49a+7b+c= ,
,
解之得,a=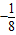 ,b=
,b= ,
,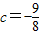 ,
,
∴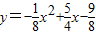 ,
,
当y=0时,x1=9,x2=1(舍去)
即D(9,0),
∴5≤x≤9;
(3)由题可知,
EG=CF=2,ED=9-5=4,
∴GD=2,
即小明从点A滑水面上点D处时,他所滑过的水平距离d=2m.
点评:此题主要考查了反比例函数和二次函数的基本性质和概念,以及用待定系数法求函数的解析式难易程度适中.
(2)由(1)知,抛物线顶点坐标已知,可列两个关系式,又C点坐标已知则可列一个关于a、b、c的方程组,进而求出解析式.
解答:解:(1)∵BE=2,B到y轴的距离是5,
∴B点坐标为(5,2),
若设反比例解析式为y=
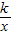 ,
,则k=10,
∴
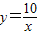 ,
,当y=5时,x=2即A点之比为(2,5),
∴2≤x≤5;
(2)设二次函数解析式为y=ax2+bx+c,
由题意可知,顶点坐标为(5,2),C点坐标为(7,
 ),
),∴
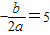 ,
,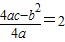 ,
,?49a+7b+c=
 ,
,解之得,a=
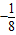 ,b=
,b= ,
,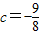 ,
,∴
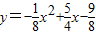 ,
,当y=0时,x1=9,x2=1(舍去)
即D(9,0),
∴5≤x≤9;
(3)由题可知,
EG=CF=2,ED=9-5=4,
∴GD=2,
即小明从点A滑水面上点D处时,他所滑过的水平距离d=2m.
点评:此题主要考查了反比例函数和二次函数的基本性质和概念,以及用待定系数法求函数的解析式难易程度适中.

练习册系列答案
相关题目
 m,与点B的水平距离CF=2m.
m,与点B的水平距离CF=2m.