题目内容
如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
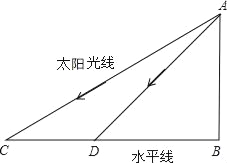
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
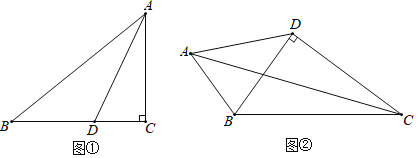
某校初二年级数学考试,(满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分布直方图和频数、频率分布表,请你根据图表提供的信息,解答下列问题:
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
(1)频数、频率分布表中a= ,b= ;(答案直接填在题中横线上)
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.
收集数据 从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
排球 10 9.5 9.5 10 8 9 9.5 9
7 10 4 5.5 10 9.5 9.5 10
篮球 9.5 9 8.5 8.5 10 9.5 10 8
6 9.5 10 9.5 9 8.5 9.5 6
整理、描述数据 按如下分数段整理、描述这两组样本数据:
4.0≤x<5.5 | 5.5≤x<7.0 | 7.0≤x<8.5 | 8.5≤x<10 | 10 | |
排球 | 1 | 1 | 2 | 7 | 5 |
篮球 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据 两组样本数据的平均数、中位数、众数如下表所示:
项目 | 平均数 | 中位数 | 众数 |
排球 | 8.75 | 9.5 | 10 |
篮球 | 8.81 | 9.25 | 9.5 |
得出结论
(1)如果全校有160人选择篮球项目,达到优秀的人数约为_____人;
(2)初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.
你同意______ 的看法,理由为__________.(至少从两个不同的角度说明推断的合理性)


 B.
B.  C.
C.  D.
D. 
 ,则随机摸出一个黄球的概率为( )
,则随机摸出一个黄球的概率为( ) B.
B. 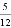 D.
D.