Question

如图，AB是⊙O的直径，⊙O的周长为l．把AB分成n条相等的线段，以每条线段为直径分别画小圆，计算每个小圆的周长l_n：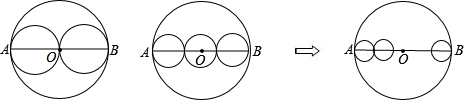

设AB=a，那么⊙O的周长l=πa．
当n=2时，AB等分成两段，每个小圆的直径为

1

2

a，周长l2=

1

2

a•π=

1

2

l；
当n=3时，l₃=

 

；当n=4时，l₄=

 

；…
由此猜想，当把AB分成n条相等的线段时，每个小圆的周长l_n=

 

；
类似地，如果设⊙O的面积为S，那么当把AB分成n条相等的线段时，每个小圆的面积是

 

（用n、S来表示）．

Answer 1

分析：利用已知条件直接求出当n=3时，l₃=

a

3

π=

1

3

πa=

1

3

l，进而得出l₄与l_n，根据当把AB分成n条相等的线段时圆的半径可得出圆的面积．

解答：解：根据已知条件：
∵AB=a，那么⊙O的周长l=πa，当n=2时，AB等分成两段，每个小圆的直径为

1

2

a，周长l2=

1

2

a•π=

1

2

l；
∴当n=3时，l₃=

a

3

π=

1

3

πa=

1

3

l，
同理可得：l₄=

1

4

l，l_n=

1

n

l，
当⊙O的面积为S=

a 2

4

π，
那么当把AB分成n条相等的线段时，每个小圆的面积是：S_n=π(

a

2n

) 2=（

1

n

）²S．
故答案为：

1

3

l，l₄=

1

4

l，l_n=

1

n

l，（

1

n

）²S．

点评：此题主要考查了圆的周长求法与圆的面积求法，发现并得出AB分成n条相等的线段时周长的变化规律是解决问题的关键．