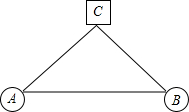
题目内容
如图：在A、B两城市之间有一风景胜地C，从A到B可选择线路①“A→C→B”或线路②“A→B”，为了节省时间，尽快从A城到达B城，应该选择线路________，这里用到的数学原理是________．
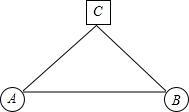
② “两点之间，线段最短”，或者“三角形任意两边的和大于第三边”
分析：需应用两点间线段最短定理来回答．
解答：设AB=c，AC=b，BC=a．
则线路①：从A城到达B城所走的路程是b+a；
线路②：从A城到达B城所走的路程是c；
∵在△ABC中，b+a＞c；
∴两点之间线段AB最短，故应该选择线路②；
故答案是：②；“两点之间，线段最短”，或者“三角形任意两边的和大于第三边”．
点评：本题考查了线段的性质：两点间线段最短、三角形三边关系．三角形任意两边的和大于第三边．
分析：需应用两点间线段最短定理来回答．
解答：设AB=c，AC=b，BC=a．
则线路①：从A城到达B城所走的路程是b+a；
线路②：从A城到达B城所走的路程是c；
∵在△ABC中，b+a＞c；
∴两点之间线段AB最短，故应该选择线路②；
故答案是：②；“两点之间，线段最短”，或者“三角形任意两边的和大于第三边”．
点评：本题考查了线段的性质：两点间线段最短、三角形三边关系．三角形任意两边的和大于第三边．
练习册系列答案
灵星计算小达人系列答案
相关题目
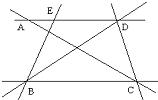23、如图所示，A、B、C、D、E五个城市，它们之间原有道路相通，现在打算在C、E两城市之间沿直线再修建一条公路，这条公路与原公路的交叉处必须设立交桥，问怎样确定立交桥的位置？应架设几座立交桥？
米为半径的圆形区域内有古迹和地下文物，现要在A、B两城市修建一条笔直的高速公路．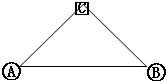
23、如图：在A、B两城市之间有一风景胜地C，从A到B可选择线路①“A→C→B”或线路②“A→B”，为了节省时间，尽快从A城到达B城，应该选择线路