题目内容
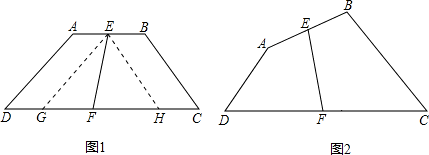
小青在研究梯形ABCD时发现,若AB∥CD,∠C+∠D=90°,且E、F是上下底AB、CD的中点,则有AD2+BC2=4EF2(提示:过E作EG∥AD,EH∥BC(如图1))
(1)小青的结论对吗?完成小青的证明.
(2)若四边形ABCD中只满足∠C+∠D=90°,且E、F是AB、CD的中点(如图2),则小青的结论还成立吗?若成立,给出证明;若不成立,说明理由.
(1)小青的结论正确.
证明如下:过点E作EG∥AD,交DF于点G,作EH∥BC,交CF于点H,
∵AB∥CD,
∴四边形ADGE是平行四边形,
∴EG=AD,DG=AE,
又EG∥AD,
∴∠EGH=∠D,
同理可得,EH=BC,CH=BE,∠EHG=∠C,
∵∠C+∠D=90°,
∴∠GEH=180°-(∠EGH+∠EHG)=180°-(∠D+∠C)=180°-90°=90°,
∵E、F上下底AB、CD的中点,
∴AE=BE,DF=CF,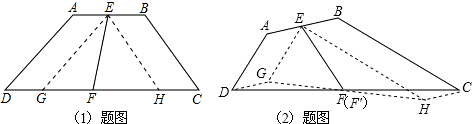
∵GF=DF-DG=DF-AE,FH=FC-CH=FC-BE,
∴GF=FH,
∴EF是Rt△EGH斜边上的中线,
∴GH=2EF,
根据勾股定理,EG2+EH2=GH2,
∴AD2+BC2=2(EF)2=4EF2,
即AD2+BC2=4EF2;
(2)成立.理由如下:
解:过点E作EG∥AD,过点D作DG∥AE,EG与DG相交于点G,过点E作EH∥BC,过点C作CH∥BE,EH与CH相交于点H,
则四边形ADGE与四边形EHCB都是平行四边形,
∴EG=AD,AE=DG,EH=BC,EB=CH,
∵DG∥AE,CH∥BE,
∴DG∥CH,
连接DH交CD于点F′,
则∠GDF′=∠HCF′,∠DGF′=∠CHF′,
∵∠C+∠D=90°,
∴∠AEG+∠BEH=∠ADG+∠BCH=∠ADC-∠GDF′+∠BCD+∠HCF′=∠ADC+∠ACD=90°,
∴∠EGH=180°-(∠AEG+∠BEH)=180°-90°=90°,
∴△EGH是直角三角形,
∵E是上底AB的中点,
∴AE=BE,
∴DG=CH,
在△DF′G和△CF′H中,
 ,
,
∴△DF′G≌△CF′H(ASA),
∴DF′=CF′,GF′=HF′,
∵点F是下底CD的中点,
∴DF=FC,
∴点F′与点F重合,
∴GH=2EF,
在Rt△EGH中,EG2+EH2=GH2,
∴AD2+BC2=(2EF)2=4EF2,
即AD2+BC2=4EF2.
分析:(1)过点E作EG∥AD,交DF于点G,作EH∥BC,交CF于点H,可得四边形ADGE是平行四边形,根据平行四边形的对边相等可得EG=AD,DG=AE,再根据两直线平行,同位角相等可得∠EGH=∠D,同理可得,EH=BC,CH=BE,∠EHG=∠C,然后证明△EGH是直角三角形,且GF=FH,再利用勾股定理即可得证;
(2)过点E作EG∥AD,过点D作DG∥AE,EG与DG相交于点G,则四边形ADGE是平行四边形,过点E作EH∥BC,过点C作CH∥BE,EH与CH相交于点H,则四边形EHCB是平行四边形,根据平行四边形的对边相等可得EG=AD,AE=DG,EH=BC,EB=CH,再根据平行公理可得DG∥CH,连接GH交CD于点F′,根据两直线平行,内错角相等可得∠GDF′=∠HCF′,∠DGF′=∠CHF′,然后结合平行四边形的对角相等证明△EGH是直角三角形,利用“角边角”证明△DF′G和△CF′H全等,根据全等三角形对应边相等可得DF′=CF′,GF′=HF′,从而得到点F′、F重合,再根据直角三角形斜边上的中线等于斜边的一半可得GH=2EF,然后利用勾股定理即可证明.
点评:本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半的性质,通过作辅助线,把AD、BC转化为同一个直角三角形的两条直角边是解题的关键,(2)通过作平行四边形,把AD、BC转化为同一个直角三角形的两条直角边不容易想到,也是本题的难点.
证明如下:过点E作EG∥AD,交DF于点G,作EH∥BC,交CF于点H,
∵AB∥CD,
∴四边形ADGE是平行四边形,
∴EG=AD,DG=AE,
又EG∥AD,
∴∠EGH=∠D,
同理可得,EH=BC,CH=BE,∠EHG=∠C,
∵∠C+∠D=90°,
∴∠GEH=180°-(∠EGH+∠EHG)=180°-(∠D+∠C)=180°-90°=90°,
∵E、F上下底AB、CD的中点,
∴AE=BE,DF=CF,

∵GF=DF-DG=DF-AE,FH=FC-CH=FC-BE,
∴GF=FH,
∴EF是Rt△EGH斜边上的中线,
∴GH=2EF,
根据勾股定理,EG2+EH2=GH2,
∴AD2+BC2=2(EF)2=4EF2,
即AD2+BC2=4EF2;
(2)成立.理由如下:
解:过点E作EG∥AD,过点D作DG∥AE,EG与DG相交于点G,过点E作EH∥BC,过点C作CH∥BE,EH与CH相交于点H,
则四边形ADGE与四边形EHCB都是平行四边形,
∴EG=AD,AE=DG,EH=BC,EB=CH,
∵DG∥AE,CH∥BE,
∴DG∥CH,
连接DH交CD于点F′,
则∠GDF′=∠HCF′,∠DGF′=∠CHF′,
∵∠C+∠D=90°,
∴∠AEG+∠BEH=∠ADG+∠BCH=∠ADC-∠GDF′+∠BCD+∠HCF′=∠ADC+∠ACD=90°,
∴∠EGH=180°-(∠AEG+∠BEH)=180°-90°=90°,
∴△EGH是直角三角形,
∵E是上底AB的中点,
∴AE=BE,
∴DG=CH,
在△DF′G和△CF′H中,
 ,
,∴△DF′G≌△CF′H(ASA),
∴DF′=CF′,GF′=HF′,
∵点F是下底CD的中点,
∴DF=FC,
∴点F′与点F重合,
∴GH=2EF,
在Rt△EGH中,EG2+EH2=GH2,
∴AD2+BC2=(2EF)2=4EF2,
即AD2+BC2=4EF2.
分析:(1)过点E作EG∥AD,交DF于点G,作EH∥BC,交CF于点H,可得四边形ADGE是平行四边形,根据平行四边形的对边相等可得EG=AD,DG=AE,再根据两直线平行,同位角相等可得∠EGH=∠D,同理可得,EH=BC,CH=BE,∠EHG=∠C,然后证明△EGH是直角三角形,且GF=FH,再利用勾股定理即可得证;
(2)过点E作EG∥AD,过点D作DG∥AE,EG与DG相交于点G,则四边形ADGE是平行四边形,过点E作EH∥BC,过点C作CH∥BE,EH与CH相交于点H,则四边形EHCB是平行四边形,根据平行四边形的对边相等可得EG=AD,AE=DG,EH=BC,EB=CH,再根据平行公理可得DG∥CH,连接GH交CD于点F′,根据两直线平行,内错角相等可得∠GDF′=∠HCF′,∠DGF′=∠CHF′,然后结合平行四边形的对角相等证明△EGH是直角三角形,利用“角边角”证明△DF′G和△CF′H全等,根据全等三角形对应边相等可得DF′=CF′,GF′=HF′,从而得到点F′、F重合,再根据直角三角形斜边上的中线等于斜边的一半可得GH=2EF,然后利用勾股定理即可证明.
点评:本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半的性质,通过作辅助线,把AD、BC转化为同一个直角三角形的两条直角边是解题的关键,(2)通过作平行四边形,把AD、BC转化为同一个直角三角形的两条直角边不容易想到,也是本题的难点.

练习册系列答案
相关题目