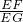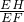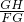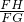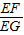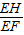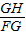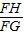题目内容
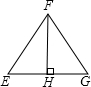
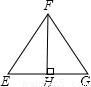
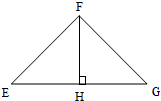 如图,在△EFG中,∠EFG=90°,FH⊥EG,下面等式中,错误的是( )
如图,在△EFG中,∠EFG=90°,FH⊥EG,下面等式中,错误的是( )A、sinG=
| ||
B、sinG=
| ||
C、sinG=
| ||
D、sinG=
|
分析:先根据同角的余角相等得出∠G=∠EFH,再根据三角函数的定义求解即可.
解答:解:∵在△EFG中,∠EFG=90°,FH⊥EG,
∴∠E+∠G=90°,∠E+∠EFH=90°,∴∠E=∠G,
∴sinG=sin∠EFH=
=
=
.
故选C.
∴∠E+∠G=90°,∠E+∠EFH=90°,∴∠E=∠G,
∴sinG=sin∠EFH=
| EF |
| EG |
| EH |
| EF |
| FH |
| FG |
故选C.
点评:本题利用了同角的余角相等和锐角三角函数的定义解答,属较简单题目.

练习册系列答案
相关题目
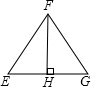 如图,在△EFG中,∠EFG=90°,FH⊥EG,下面等式中,错误的是
如图,在△EFG中,∠EFG=90°,FH⊥EG,下面等式中,错误的是