��Ŀ����
����Ŀ����ͼ�����ı���ABCD�У�AB��CD����BCD��90����AB��AD��10cm��BC��8cm����P�ӵ�A��������3cm��s���ٶ�������ABCD�����˶�����Q�ӵ�D��������2cm��s���ٶ����߶�DC���C�˶�����֪P��Q����ͬʱ����������Q�����Cʱ��P��Qֹͣ�˶������˶�ʱ��Ϊt��s����

��1������CD�ij���
��2�������ı���PBQDΪƽ���ı���ʱ�����ı���PBQD���ܳ���
��3��������P������BCD���˶�ʱ���Ƿ����ijһʱ�̣�ʹ����BPQ�����Ϊ16cm2�������ڣ����������������t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1����16cm����2������8��8��cm����3������6��
��������
�����������1����������A��AM��BC��DC��M������ƽ���ı��ε����ʵó�MC��AB��10cm��AM��BC��8cm������Rt��ADM�Ĺ��ɶ������DM�ij��ȣ�Ȼ��ó��𰸣���2�������ı���PBQDΪƽ���ı���ʱ��PB��DQ��PB��DQ����������ó�PB����10��3t��cm��DQ��2tcm���Ӷ����t��ֵ��Ȼ��ó��ı��ε��ܳ�����3�������������������⣬������P���߶�BC�ϣ�����t��6��������P���߶�CD�ϣ��ҵ�P�ڵ�Q���Ҳ࣬��6��t����������P���߶�CD�ϣ��ҵ�P�ڵ�Q����࣬����t��8�����������ε�����г����̣����t��ֵ.
�����������1��������A��AM��BC��DC��M����ͼ��
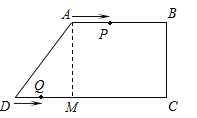
��AB��CD��
���ı���ABCM��ƽ���ı��Σ�
��MC��AB��10cm��AM��BC��8cm��
�ߡ�BCD��90�������AMD��90����
��AD��10cm��
��DM������6��cm����
��CD��DM��MC��10cm��6cm��16cm��
��2�������ı���PBQDΪƽ���ı���ʱ��PB��DQ��PB��DQ�� ����Q��DC�ϣ�����P��AB�ϣ���ͼ����
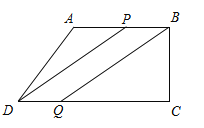
��0��t����
�������PB����10��3t��cm��DQ��2t��cm����
��10��3t��2t�����t��2���������⣩��
��ʱDQ��4 cm��
��QC��12 cm��
��BQ������4��cm����
���ı���PBQD���ܳ���2��BQ��DQ������8��8��cm��
��3��������������������ۣ�
������P���߶�BC�ϣ���ͼ��������t��6��
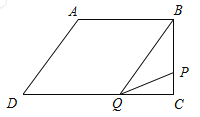
��ʱBP��3t��10��CQ��16��2t��
��S��BPQ��BPCQ����3t��10����16��2t����16��
��3t2��34t��96��0��
�ߡ�������34��2��4��3��96��4��
��t������
��t��6�����������⣩��
������P���߶�CD�ϣ��ҵ�P�ڵ�Q���Ҳࣨ��ͼ������6��t����
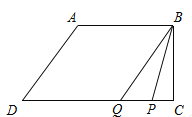
��ʱQP��34��5t��
��S��BPQ��QPBC����34��5t����8��16��
���t��6���������⣩��
������P���߶�CD�ϣ��ҵ�P�ڵ�Q����ࣨ��ͼ��������t��8��
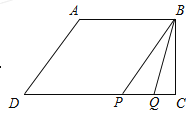
��ʱPQ��5t��34��
��S��BPQ��PQBC����5t��34����8��16��
���t�����������⣩��
���ϣ����ڷ��������ʱ�̣���t��ֵΪ����6������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij��������־Ը��С�ֶ�������������ʾ��
���䣨�꣩ | 18 | 19 | 20 | 21 | 22 |
���� | 2 | 5 | 2 | 2 | 1 |
����12����Ա�������������λ���ֱ��ǣ� ��
A.2��20��
B.2��19��
C.19�꣬20��
D.19�꣬19��