题目内容
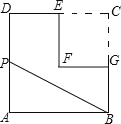
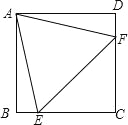
【题目】如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
【答案】(1)y=﹣![]() x+
x+![]() ;(2)m=1;(3)1≤n≤4.
;(2)m=1;(3)1≤n≤4.
【解析】
试题分析:∵在正方形ABCD中,∴AB=AD,∵AE=AF,∴在Rt△ABF和Rt△ADE中∵![]() ,∴Rt△ABF≌Rt△ADE(HL),∴BF=DE,∵EC的长为x,∴FC=x,BF=4﹣x,DE=4﹣x,∴△AEF的面积为:y=16﹣S△ABF﹣S△ADE﹣S△EFC=16﹣
,∴Rt△ABF≌Rt△ADE(HL),∴BF=DE,∵EC的长为x,∴FC=x,BF=4﹣x,DE=4﹣x,∴△AEF的面积为:y=16﹣S△ABF﹣S△ADE﹣S△EFC=16﹣![]() ×4(4﹣x)﹣
×4(4﹣x)﹣![]() ×4(4﹣x)﹣
×4(4﹣x)﹣![]() x2=﹣
x2=﹣![]() x2+4x(0<x<4).
x2+4x(0<x<4).

练习册系列答案
相关题目