题目内容
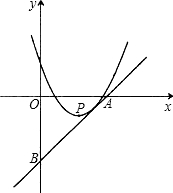 如图,已知过点(
如图,已知过点(| 3 |
| 2 |
| 7 |
| 4 |
(1)求k的值;
(2)设抛物线的顶点为P,求点P到直线AB的距离d.
分析:(1)由于点(
,一
)在直线y=kx+b上,则此点坐标满足该一次函数解析式,将其代入即可求出k、b的关系式;用k代替b后,联立抛物线的解析式,可得关于x的一元二次方程,由于两个函数只有一个公共点,那么方程的根的判别式△=0,可据此求出k的值.
(2)根据k的值,可确定直线的解析式,进而可求出A、B的坐标,也就能得到△OAB的面积;可连接OP、AP、BP,将△AOB分成△OPA、△OPB、△APB三部分,P点坐标易求得,即可得到△OPA和△OPB的面积,用d表示出△APB的面积,根据上面所得四个三角形的面积关系式,即可求出d的值.
| 3 |
| 2 |
| 7 |
| 4 |
(2)根据k的值,可确定直线的解析式,进而可求出A、B的坐标,也就能得到△OAB的面积;可连接OP、AP、BP,将△AOB分成△OPA、△OPB、△APB三部分,P点坐标易求得,即可得到△OPA和△OPB的面积,用d表示出△APB的面积,根据上面所得四个三角形的面积关系式,即可求出d的值.
解答:解:(1)∵直线过点(
,-
),
∴-
=
k+b,
即b=-
-
k;
∴y=kx-
k-
,
由
消去y,得:
x2-(4+k)x+(
k+
)=0,
∵直线与抛物线只有一个公共点,
∴△=(4+k)2-4(
k+
)=0,
解得:k=1或k=-3;
∵直线过第一、三、四象限,
∴k>0,
即k=1.
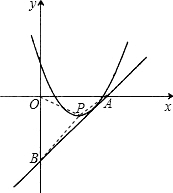
(2)由k=1,知直线AB的解析式为y=x-
;
令y=0,得x=
;
令x=0,得y=-
;
∴A(
,0),B(0,-
),
∴AB=
=
;
连接PO、PA、PB,易知抛物线顶点P(2,-1),
由S△APO+S△BPO+S△APB=S△ABO,得:
OA•1+
OB•2+
AB•d=
OA•OB,
∴d=
=
,
∴点P到直线AB的距离为
.
| 3 |
| 2 |
| 7 |
| 4 |
∴-
| 7 |
| 4 |
| 3 |
| 2 |
即b=-
| 7 |
| 4 |
| 3 |
| 2 |
∴y=kx-
| 3 |
| 2 |
| 7 |
| 4 |
由
|
x2-(4+k)x+(
| 3 |
| 2 |
| 19 |
| 4 |
∵直线与抛物线只有一个公共点,
∴△=(4+k)2-4(
| 3 |
| 2 |
| 19 |
| 4 |
解得:k=1或k=-3;
∵直线过第一、三、四象限,
∴k>0,
即k=1.
(2)由k=1,知直线AB的解析式为y=x-
| 13 |
| 4 |

令y=0,得x=
| 13 |
| 4 |
令x=0,得y=-
| 13 |
| 4 |
∴A(
| 13 |
| 4 |
| 13 |
| 4 |
∴AB=
| OA2+OB2 |
13
| ||
| 4 |
连接PO、PA、PB,易知抛物线顶点P(2,-1),
由S△APO+S△BPO+S△APB=S△ABO,得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴d=
| OA•OB-OA-2OB |
| AB |
| ||
| 8 |
∴点P到直线AB的距离为
| ||
| 8 |
点评:此题考查了函数图象交点、根的判别式以及图形面积的求法等,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知一次函数y=kx+
如图,已知一次函数y=kx+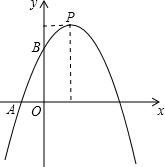 点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.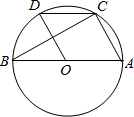 (2013•徐州模拟)如图,已知AB是⊙O的直径,BC为弦,过圆心O作OD⊥BC交弧BC于点D,连接DC,若∠DCB=32°,则∠BAC=
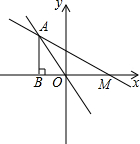
(2013•徐州模拟)如图,已知AB是⊙O的直径,BC为弦,过圆心O作OD⊥BC交弧BC于点D,连接DC,若∠DCB=32°,则∠BAC= 如图,已知△OAB中,AB=AO=20,点B的坐标为(-32,0).求过点A的反比例函数的解析式.
如图,已知△OAB中,AB=AO=20,点B的坐标为(-32,0).求过点A的反比例函数的解析式.