题目内容
现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片（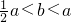
）如图1，取出两张小卡片放入大卡片内拼成的图案如图2，再重新用三张小正方形卡片放入大卡片内拼成的图案如图3．已知图3中的阴影部分的面积比图2中的阴影部分的面积大2ab-6，则小正方形卡片的面积b2=________．
2
分析：在图2中，阴影部分为正方形，其边长为2b-a，得到其面积为=（2b-a）2；在图3中，阴影部分的面积等于面积为a（a-b）的矩形面积减去面积为b（a-b）的矩形面积得到，然后根据图3中的阴影部分的面积比图2中的阴影部分的面积大2ab-6建立等量关系（a-b）2-（2b-a）2=2ab-6，去括号、移项得到b2=2．
解答：在图2中，阴影部分的面积=（2b-a）2；在图3中，阴影部分的面积=a（a-b）-b（a-b）=（a-b）2；
根据题意得，（a-b）2-（2b-a）2=2ab-6，
a2-2ab+b2-4b2+4ab-a2=2ab-6，
∴b2=2．
故答案为：2．
点评：本题考查了整式的混合运算：先进行整式的乘方运算，再进行整式的乘除运算，然后进行整式的加减运算（即合并同类项）．也考查了观察图形的能力．
分析：在图2中，阴影部分为正方形，其边长为2b-a，得到其面积为=（2b-a）2；在图3中，阴影部分的面积等于面积为a（a-b）的矩形面积减去面积为b（a-b）的矩形面积得到，然后根据图3中的阴影部分的面积比图2中的阴影部分的面积大2ab-6建立等量关系（a-b）2-（2b-a）2=2ab-6，去括号、移项得到b2=2．
解答：在图2中，阴影部分的面积=（2b-a）2；在图3中，阴影部分的面积=a（a-b）-b（a-b）=（a-b）2；
根据题意得，（a-b）2-（2b-a）2=2ab-6，
a2-2ab+b2-4b2+4ab-a2=2ab-6，
∴b2=2．
故答案为：2．
点评：本题考查了整式的混合运算：先进行整式的乘方运算，再进行整式的乘除运算，然后进行整式的加减运算（即合并同类项）．也考查了观察图形的能力．
练习册系列答案
相关题目
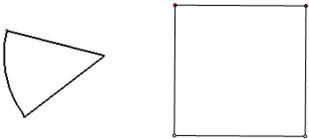
）如图1，取出两张小卡片放入大卡片内拼成的图案如图2，再重新用三张小正方形卡片放入大卡片内拼成的图案如图3．已知图3中的阴影部分的面积比图2中的阴影部分的面积大2ab-6，则小正方形卡片的面积b2=（ ）。