题目内容
某污水处理公司为学校建一座三级污水处理池,平面图形为矩形,面积为200平方米(平面图如图所示的ABCD).已知池的外围墙建造单价为每米400元.中间两条隔墙建造单价每米300元,池底建造的单价为每平方米80元(池墙的厚度不考虑)(1)如果矩形水池恰好被隔墙分成三个正方形,试计算此项工程的总造价(精确到100元);
(2)如果矩形水池的形状不受(1)中长、宽的限制,问预算45600元总造价,能否完成此项工程?试通过计算说明理由;
(3)请估算此项工程的最低造价(多出部分只要不超过100元就有效).

【答案】分析:(1)先根据面积求得矩形的长和宽,总造价=外围的长度×400+两条隔墙的长度和×300+矩形面积×80;
(2)设出一边长,根据面积得到另一边长,代入(1)得到的代数式,看有无解即可;
(3)在(2)的基础上增加费用,得到有解,找到造价最低的可能即可.
解答:解:(1)设AB=x,则AD=3x,
依题意3x2=200,
x≈8.165.
设总造价W元.
W=8x×400+2x×300+200×80=3800x+16000=47000(元)…(2分);
(2)AB=x,则AD=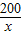 ,
,
所以(2x+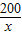 ×2)×400+2x×300+80×200=45600.
×2)×400+2x×300+80×200=45600.
整理,得7x2-148x+800=0.
此时求根公式中的被开方式=一496<0,
所以此方程无实数解,即预算45600元不能完成此项工程. …(6分)
(3)估算:造价45800元.(2x+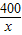 )×400+600x+16000=45800.
)×400+600x+16000=45800.
整理,得7x2-149x+800=0.
此时求根公式中的被开方式=-199<0,仍不够.
造价46000元,同法可得7x2-150x+800=0.此时求根公式中的被开方式=100>0,够了.
造价45900元,可得求根公式中的被开方式=一49.75<0,不够.最低造价为46000元.…(10分)
点评:考查一元二次方程的应用;得到总造价的等量关系是解决本题的易错点;会利用求根公式判断预算结果正确与否是解决本题的难点.
(2)设出一边长,根据面积得到另一边长,代入(1)得到的代数式,看有无解即可;
(3)在(2)的基础上增加费用,得到有解,找到造价最低的可能即可.
解答:解:(1)设AB=x,则AD=3x,
依题意3x2=200,
x≈8.165.
设总造价W元.
W=8x×400+2x×300+200×80=3800x+16000=47000(元)…(2分);
(2)AB=x,则AD=
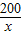 ,
,所以(2x+
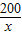 ×2)×400+2x×300+80×200=45600.
×2)×400+2x×300+80×200=45600.整理,得7x2-148x+800=0.
此时求根公式中的被开方式=一496<0,
所以此方程无实数解,即预算45600元不能完成此项工程. …(6分)
(3)估算:造价45800元.(2x+
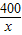 )×400+600x+16000=45800.
)×400+600x+16000=45800.整理,得7x2-149x+800=0.
此时求根公式中的被开方式=-199<0,仍不够.
造价46000元,同法可得7x2-150x+800=0.此时求根公式中的被开方式=100>0,够了.
造价45900元,可得求根公式中的被开方式=一49.75<0,不够.最低造价为46000元.…(10分)
点评:考查一元二次方程的应用;得到总造价的等量关系是解决本题的易错点;会利用求根公式判断预算结果正确与否是解决本题的难点.

练习册系列答案
相关题目
 度不考虑)
度不考虑)


