题目内容
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(4,4),反比例函数![]() 的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
(1)求k的值;
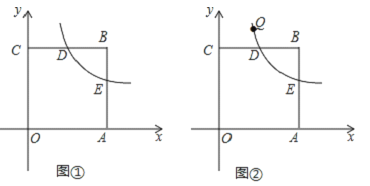
(2)如图①,若点P是x轴上的动点,连接PE,PD,DE,当△DEP的周长最短时,求点P的坐标;
(3)如图②,若点Q(x,y)在该反比例函数图象上运动(不与D重合),过点Q作QM⊥y轴,垂足为M,作QN⊥BC所在直线,垂足为N,记四边形CMQN的面积为S,求S关于x的函数关系式,并写出x的取值范围.
【答案】(1)8 ;(2)(![]() );(3)S=8-4x,0<x<2;S=4x-8,x>2
);(3)S=8-4x,0<x<2;S=4x-8,x>2
【解析】
(1)首先根据题意求出C点的坐标,然后根据中点坐标公式求出D点坐标,由反比例函数y=![]() (x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
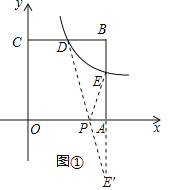
(2)根据轴对称的性质找到点P的位置:作点E关于x轴的对称点E′,连接DE′,交x轴于点P,求得直线DE′与x轴的交点坐标即可;
(3)分两步进行解答,①当Q在直线BC的上方时,即0<x<2,如图1,根据S四边形CMQN=CNQD列出S关于x的解析式,②当Q在直线BC的下方时,即x>2,如图2,依然根据S四边形CMQN=CNQD列出S关于x的解析式.
(1)如图①,
∵正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),
∴C(0,4),
∵D是BC的中点,
∴D(2,4),
∵反比例函数y=![]() (x>0,k≠0)的图象经过点D,
(x>0,k≠0)的图象经过点D,
∴k=8;
(2)如图①,作点E关于x轴的对称点E′,连接DE′,交x轴于点P,
把x=4代入y=![]() ,得y=2,则E(4,2),
,得y=2,则E(4,2),
故点E关于x轴对称的点E′(4,-2),
设直线DE′的方程为y=kx+b(k≠0),
将D(2,4),E′(4,-2)分别代入得到:![]() ,
,
解得![]() ,
,
故直线DE′的方程为y=-3x+10,
当y=0时,x=![]() ,
,
即P(![]() ,0);
,0);
(3)如图②,
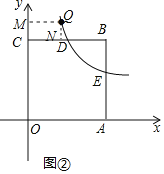
当Q在直线BC的上方时,即0<x<2,
如图1,∵点Q(x,y)在该反比例函数的图象上运动,
∴y=![]() ,
,
∴S四边形CMQN=CNQD=x(![]() -4)=8-4x(0<x<2),
-4)=8-4x(0<x<2),
如图③,
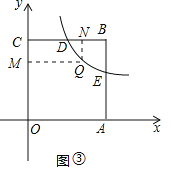
当Q在直线BC的下方时,即x>4,同理求出S四边形CMQN=CNQD=x(4-![]() )=4x-8(x>2),
)=4x-8(x>2),
综上S=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某中学七、八年级各选![]() 名同学参加“创全国文明城市”知识竞赛,计分
名同学参加“创全国文明城市”知识竞赛,计分![]() 分制,选手得分均为整数,成绩达到
分制,选手得分均为整数,成绩达到![]() 分或
分或![]() 分以上为合格,达到
分以上为合格,达到![]() 分或
分或![]() 分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得
分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得![]() 分、
分、![]() 分选手人数分别为
分选手人数分别为![]() ,
,![]() .
.
队列 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
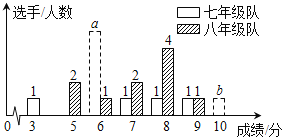
(1)根据图表中的数据,求![]() ,
,![]() 的值.
的值.
(2)直接写出表中的![]() ,
,![]() .
.
(3)你是八年级学生,请你给出两条支持八年级队成绩好的理由.