题目内容
【题目】如图，在平面直角坐标系中，存在直线y1＝2x和直线y2＝－x＋3
(1) 直接写出直线y2＝－x＋3与坐标轴的交点坐标：__________、__________
(2) 求出直线y1＝2x和直线y2＝－x＋3的交点坐标
(3) 结合图象，直接写出0＜y2＜y1的解集：_________________
【答案】（1）（3，0）（0，3）；（2）交点坐标（1，2）；（3）1＜x＜3
【解析】试题分析：（1）令y2＝－x＋3中x=0求得y值即可得直线与y轴交点坐标，令y0求得x值即可得直线与x轴交点坐标；（2）由直线y1＝2x和直线y2＝－x＋3联立得方程组，解方程组即可得两直线的交点坐标；（3）由图像可知当0＜y2＜y1，即在 x轴上方及直线y1下方的图象所对应的区间，结合（1）（2）可得.
试题解析：（1）令y=0，得x=3，令x=0，得y=3，所以直线和x轴交点为（3，0），和y轴交点为（0，3）；
（2）由
，解得
，所以两直线交点坐标为（1，2）；
（3）
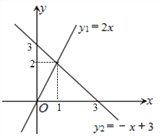
由图象可知0＜y2＜y1的解集为1＜x＜3.
练习册系列答案
相关题目