题目内容
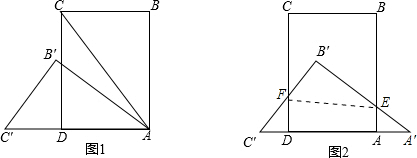
(2013•南昌模拟)矩形ABCD中AB=8,BC=6,∠ACB=53°;将△ABC绕点A逆时针旋转得到△AB′C′,使点C′落在AD延长线上(图1).
(1)求∠B′AC的度数与C′D的长度;
(2)如图2 将△AB′C′向右平移得△A′B′C′,两直角边与矩形相交于点E、F;在平移的过程中出现了△AA′E≌△DFC′;求此时平移的距离AA′.(设AA′=x)
(3)当平移的距离是多少时,能使△B′EF与原△ABC相似.
(1)求∠B′AC的度数与C′D的长度;
(2)如图2 将△AB′C′向右平移得△A′B′C′,两直角边与矩形相交于点E、F;在平移的过程中出现了△AA′E≌△DFC′;求此时平移的距离AA′.(设AA′=x)
(3)当平移的距离是多少时,能使△B′EF与原△ABC相似.

分析:(1)根据矩形的性质得出BC=AD=6,BC∥AD,∠B=90°,求出∠BCA=∠CAD=53°,∠BAC=∠B′AC′=37°,即可求出答案;勾股定理求出AC=10=AC′,求出C′D即可;
(2)证△A′AE∽△A′B′C′求出AE=
,根据△AA′E≌△DFC′,得出AE=C′D,得出方程10-6-x=
x,求出方程的解即可;
(3)根据△A′AE∽△A′B′C′求出A′E=
x,B′E=8-
x,根据△C′DF∽△A′B′C′求出C′F=
(4-x),B′F=6-
(4-x),当满足B′E:B′F=6:8或B′E:B′F=8:6,两三角形相似,代入求出即可.
(2)证△A′AE∽△A′B′C′求出AE=
| 3x |
| 4 |
| 3 |
| 4 |
(3)根据△A′AE∽△A′B′C′求出A′E=
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
解答:解:(1)∵四边形ABCD是矩形,
∴BC=AD=6,BC∥AD,∠B=90°,
∴∠BCA=∠CAD=53°,∠BAC=∠B′AC′=90°-53°=37°,
∴∠B′AC=53°-37°=16°,
在Rt△CBA中,AB=8,BC=6,由勾股定理得:AC=10=AC′,
∴C′D=10-6=4;
(2)∵∠A′=∠A′,∠C′B′A′=∠EAA′=90°,
∴△A′AE∽△A′B′C′,
∴
=
,
∴
=
,
∴AE=
,
∵△AA′E≌△DFC′,
∴AE=C′D,
∴10-6-x=
x,
x=
,
即此时平移的距离AA′是
;
(3)
∵△A′AE∽△A′B′C′,
∴
=
,
∴
=
,
∴A′E=
x,
∴B′E=8-
x,
同理由△C′DF∽△A′B′C′求出C′F=
(4-x),
∴B′F=6-
(4-x),
当满足B′E:B′F=6:8或B′E:B′F=8:6时,能使△B′EF与原△ABC相似
即(8-
x):[6-
(4-x)]=6:8或(8-
x):[(6-
(4-x)]=8:6,
解得:x=3.4或x=
,
∴当平移的距离是3.4或x=
时,能使△B′EF与原△ABC相似.
∴BC=AD=6,BC∥AD,∠B=90°,
∴∠BCA=∠CAD=53°,∠BAC=∠B′AC′=90°-53°=37°,
∴∠B′AC=53°-37°=16°,
在Rt△CBA中,AB=8,BC=6,由勾股定理得:AC=10=AC′,
∴C′D=10-6=4;
(2)∵∠A′=∠A′,∠C′B′A′=∠EAA′=90°,
∴△A′AE∽△A′B′C′,
∴
| AE |
| C′B′ |
| AA′ |
| A′B′ |
∴
| AE |
| 6 |
| x |
| 8 |
∴AE=
| 3x |
| 4 |
∵△AA′E≌△DFC′,
∴AE=C′D,
∴10-6-x=
| 3 |
| 4 |
x=
| 16 |
| 7 |
即此时平移的距离AA′是
| 16 |
| 7 |
(3)

∵△A′AE∽△A′B′C′,
∴
| A′E |
| A′C′ |
| AA′ |
| A′B′ |
∴
| A′E |
| 10 |
| x |
| 8 |
∴A′E=
| 5 |
| 4 |
∴B′E=8-
| 5 |
| 4 |
同理由△C′DF∽△A′B′C′求出C′F=
| 5 |
| 3 |
∴B′F=6-
| 5 |
| 3 |
当满足B′E:B′F=6:8或B′E:B′F=8:6时,能使△B′EF与原△ABC相似
即(8-
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
解得:x=3.4或x=
| 64 |
| 25 |
∴当平移的距离是3.4或x=
| 64 |
| 25 |
点评:本题考查了矩形性质,勾股定理,相似三角形的性质和判定的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目
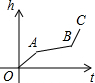 (2013•南昌模拟)均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( )
(2013•南昌模拟)均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( )
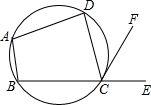 (2013•南昌模拟)如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若CF平分∠DCE,则∠DCF的大小是( )
(2013•南昌模拟)如图,四边形ABCD是圆内接四边形,∠BAD=108°,E是BC延长线上一点,若CF平分∠DCE,则∠DCF的大小是( )