题目内容
【题目】如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
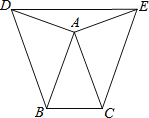
(1)求证:AB=AC;
(2)若∠DAE=2∠ABC=140°,求∠BAD的度数.
【答案】(1)证明见解析(2)90°
【解析】
试题分析:(1)由等腰三角形的性质可知∠ADE=∠AED,从而可得到∠ADB=∠AEC,依据AAS可证明△ADB≌△AEC;
(2)由题意可知:∠ABC=70°,由等腰三角形的性质可知∠ABC=∠ACB=70°,由三角形内角和定理可知∠BAC=40°,由△ADB≌△AEC可知∠DAB=∠EAC,故此∠BAD=![]() (360°﹣140°﹣40°)=90°.
(360°﹣140°﹣40°)=90°.
(1)证明:∵AD=AE,
∴∠ADE=∠AED.
∵∠BDE=∠CED,
∴∠BDE﹣∠ADE=∠CED﹣∠AED.
∴∠ADB=∠AEC.
在△ADB和△AEC中,
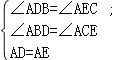
∴△ADB≌△AEC.
∴AB=AC.
(2)解:∵2∠ABC=140°,
∴∠ABC=70°.
∵AB=AC,
∴∠ABC=∠ACB=70°.
∴∠BAC=180°﹣∠ABC﹣∠ACB=40°.
∵△ADB≌△AEC,
∴∠DAB=∠EAC.
∵∠DAE=140°,
∴∠BAD=![]() (360°﹣140°﹣40°)=90°.
(360°﹣140°﹣40°)=90°.

练习册系列答案
相关题目