��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P��a��b���͵�Q��a��b'�����������¶��壺
��b'=![]() ����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
����Ƶ�QΪ��P���ޱ�㣮���磺�㣨3����2�����ޱ��������ǣ�3����2�����㣨��1��5�����ޱ��������ǣ���1����5����
��1���ٵ㣨��![]() ��1�����ޱ����������� ����
��1�����ޱ����������� ����
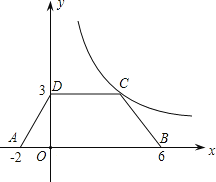
���ڵ�A����1��2����B����2����1������һ�����Ǻ���y=![]() ͼ����ijһ��������㣬��������� ����
ͼ����ijһ��������㣬��������� ����
��2������P�ں���y=��x+3��ͼ���ϣ�����2��x��6ʱ�������ޱ��Q��������b'��ȡֵ��Χ��
��3������P�ڹ���x�Ķ��κ���y=x2��2tx+t2+t��ͼ���ϣ����ޱ��Q��������b'��ȡֵ��Χ��b'��m��b'��n������m��n����s=m��n����s����t�ĺ�������ʽ��s��ȡֵ��Χ��
���𰸡���1��������![]() ����1������A����2������2��x��6ʱ����5��b���2����3��s����t�ĺ�������ʽΪs=t2+1��t��1����s��ȡֵ��Χ��s��2��
����1������A����2������2��x��6ʱ����5��b���2����3��s����t�ĺ�������ʽΪs=t2+1��t��1����s��ȡֵ��Χ��s��2��
��������
��1����ֱ�Ӹ����ޱ��Ķ���ֱ�ӵó��𰸣�
�ڵ㣨-1��-2���ڷ���������ͼ���ϣ��㣨-1��-2�����ޱ��Ϊ��-1��2�����ݴ˵õ��𰸣�
��2�����������֪y=-x+3��x��-2��ͼ���ϵĵ�P���ޱ��Q���ں���y=![]() ��ͼ���ϣ����ͼ�ɵõ��𰸣�
��ͼ���ϣ����ͼ�ɵõ��𰸣�
��3���������y=x2-2tx+t2+t�������꣬���t��1�Ĺ�ϵȷ��y����ֵ��������m��n��ʾ��s������t��ȡֵ��Χ���s��ȡֵ��Χ��
��1���ٸ����ޱ��Ķ����֪��㣨��![]() ��1�����ޱ�������Ϊ����
��1�����ޱ�������Ϊ����![]() ����1����
����1����
������1����2���ޱ��Ϊ����1��2������������ǵ�A��
��2�������⣬y=��x+3��x�ݩ�2��ͼ���ϵĵ�P���ޱ��Q���ں���y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
��x=��2ʱ��y=��2��3=��5��
��x=1ʱ��y=��1+3=2��
��x=6ʱ��y=��6+3=��3��
�൱��2��x��6ʱ����5��b���2��
��3����y=x2��2tx+t2+t=��x��t��2+t��
�ඥ������Ϊ��t��t����
��t��1��b����ȡֵ��Χ��b���m��b�䣼n�������ⲻ����
��t��1����x��1ʱ��y����СֵΪt����m=t��
��x��1ʱ��y��ֵС�ک�[��1��t��2+t]����n=��[��1��t��2+t]��
��s=m��n=t+��1��t��2+t=t2+1��
��s����t�ĺ�������ʽΪs=t2+1��t��1����
��t=1ʱ��sȡ��Сֵ2��
��s��ȡֵ��Χ��s��2��

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�