题目内容
(2012•翔安区模拟)(1)如图1,已知线段AB,请用直尺和圆规作出线段AB的垂直平分线(不写画法,保留作图痕迹);
(2)计算:(-1)0+2sin60°+
-|1-
|;
(3)如图2,已知AB∥CD,直线MN交AB于M,交CD于N,ME平分∠AMN,NF平分∠DNM,求证:EM∥FN.

(2)计算:(-1)0+2sin60°+
| 16 |
| 3 |
(3)如图2,已知AB∥CD,直线MN交AB于M,交CD于N,ME平分∠AMN,NF平分∠DNM,求证:EM∥FN.

分析:(1)分别以A、B为圆心,大于
AB长为半径画弧,两弧交于M、N两点,过MN画直线即可;
(2)此题涉及到零指数幂、特殊角的三角函数、二次根式的化简、绝对值,根据各知识点进行计算后,再进行加减即可;
(3)首先根据AB∥CD,可得∠AMN=∠DNM,再根据ME平分∠AMN,NF平分∠DNM,可得∠1=
∠AMN,∠2=
∠DNM,进而得到∠1=∠2,再根据内错角相等,两直线平行可得EM∥FN.
| 1 |
| 2 |
(2)此题涉及到零指数幂、特殊角的三角函数、二次根式的化简、绝对值,根据各知识点进行计算后,再进行加减即可;
(3)首先根据AB∥CD,可得∠AMN=∠DNM,再根据ME平分∠AMN,NF平分∠DNM,可得∠1=
| 1 |
| 2 |
| 1 |
| 2 |
解答: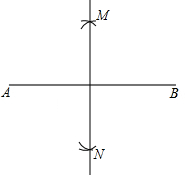 解:(1)如图所示:
解:(1)如图所示:
(2)解:原式=1+
+4-
+1,
=6;
(3)证明:
如图,∵AB∥CD,
∴∠AMN=∠DNM,
又∵ME平分∠AMN,NF平分∠DNM,
∴∠1=
∠AMN,∠2=
∠DNM,
∴∠1=∠2,
∴EM∥FN.
 解:(1)如图所示:
解:(1)如图所示:(2)解:原式=1+
| 3 |
| 3 |
=6;
(3)证明:
如图,∵AB∥CD,
∴∠AMN=∠DNM,
又∵ME平分∠AMN,NF平分∠DNM,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
∴EM∥FN.
点评:此题主要考查了线段垂直平分线的性质,实数的运算,以及平行线的性质与判定,关键是熟练掌握基本作图的方法,以及零指数幂、特殊角的三角函数、二次根式的化简、绝对值的计算方法.

练习册系列答案
相关题目