题目内容
如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为80.8千米／时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小．⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )
| A．1个 | B．2个 | C．3个 | D．4个 |
A.
解析试题分析：根据图象对每条进行分别判断即可，行驶的最远距离是120千米，共行驶240千米，共用时间是4.5小时．
①行驶的最远距离是120千米，共行驶240千米，故此选项错误；
②根据图象从1.5时到2时，是停留时间，停留0.5小时，故此选项正确；
③汽车在整个行驶过程中的平均速度为
千米/时，故此选项错误；
④汽车自出发后3小时至4.5小时之间路程与时间成一次函数关系，因而速度不变．故此选项错误；
⑤∵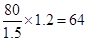
，因为汽车回来途中也有离出发地64千米的时候；故此选项错误．
故正确的说法是：②．
故选A.
考点: 函数的图象．
练习册系列答案
相关题目
x＋m和y＝
x＋n的图象都经过点A(－2，0)，且与y轴分别交于B、C两点，那么△ABC的面积是 ( )如果
,
,则函数
的图象一定不经过（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
关于直线y=－2x，下列结论正确的是（ ）
| A．图象必过点（1,2） | B．图象经过第一、三象限 |
| C．与y=-2x+1平行 | D．y随x的增大而增大 |
线段
，当
的值由
增加到2时，该线段运动所经过的平面区域的面积为（ ）
| A．6 | B．8 | C．9 | D．10 |
如图，直线y=kx+b交坐标轴于A（﹣2，0），B（0，3）两点，则不等式kx+b＞0的解集是
| A．x＞3 | B．﹣2＜x＜3 | C．x＜﹣2 | D．x＞﹣2 |
的图象相交于A、B两点，若点A的坐标为(2，1)，则点B的坐标是 ( )
若一次函数
的图象交
轴于正半轴，且的值随
值的增大而减小，则（ ）
A． | B． | C． | D． |