题目内容
已知半径为R的圆中一条弧所对的圆周角为60°,那么它所对的弦长为
- A.
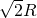
- B.2
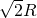
- C.

- D.2

C
分析:画出图形,作直径AD,连接BD,由圆周角定理得出∠C=∠D=60°,求出∠ABD=90°,根据sin∠D=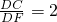 求出AB即可.
求出AB即可.
解答: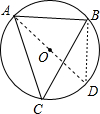 作直径AD,连接BD,
作直径AD,连接BD,
由圆周角定理得:∠C=∠D=60°,
∵AB是⊙O直径,
∴∠ABD=90°,
∴sin∠D=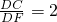 ,
,
∴AB=AD•sin60°=2R× =
= R.
R.
故选C.
点评:本题考查了圆周角定理和解直角三角形,关键是构造直角三角形,题目比较好.
分析:画出图形,作直径AD,连接BD,由圆周角定理得出∠C=∠D=60°,求出∠ABD=90°,根据sin∠D=
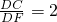 求出AB即可.
求出AB即可.解答:
 作直径AD,连接BD,
作直径AD,连接BD,由圆周角定理得:∠C=∠D=60°,
∵AB是⊙O直径,
∴∠ABD=90°,
∴sin∠D=
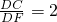 ,
,∴AB=AD•sin60°=2R×
 =
= R.
R.故选C.
点评:本题考查了圆周角定理和解直角三角形,关键是构造直角三角形,题目比较好.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
已知点P是半径为5的圆O内一定点,且OP=4,则过点P的所有弦中,弦长可能取到的整数值为( )
| A、5,4,3 | B、10,9,8,7,6,5,4,3 | C、10,9,8,7,6 | D、12,11,10,9,8,7,6 |
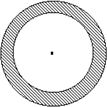 游戏是公平的?(只需写出小圆半径,不必说明原因)
游戏是公平的?(只需写出小圆半径,不必说明原因)


