题目内容
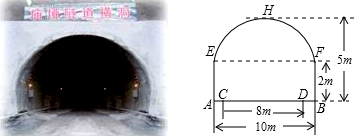
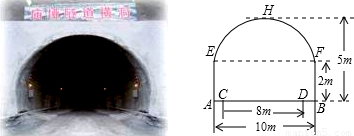
路在山腹行是沪蓉西高速公路的显著特点之一，全线共有隧道37座，共计长达742421.2米．下图是正在修建的庙垭隧道的截面，截面是由一抛物线和一矩形构成，其行车道CD总宽度为8米，隧道为单行线2车道．（1）建立恰当的平面直角坐标系，并求出隧道拱抛物线的解析式；
（2）在隧道拱的两侧距地面3米高处各安装一盏路灯，在（1）的平面直角坐标系中用坐标表示其中一盏路灯的位置；
（3）为了保证行车安全，要求行驶车辆顶部（设为平顶）与隧道拱在竖直方向上高度之差至少有0.5米．现有一辆汽车，装载货物后，其宽度为4米，车载货物的顶部与路面的距离为2.5米，该车能否通过这个隧道？请说明理由．
【答案】分析：本题是抛物线的问题，建立适当坐标系，把有关数据转化为相应点的坐标，选择合适的抛物线解析式，是解本题的关键．难点是（3）对能否通过的理解．
解答：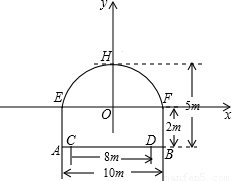
解：（1）如图，若以EF所在直线为x轴，经过H且垂直于EF的直线为y轴，建立平面直角坐标系，
则E（-5，0），F（5，0），H（0，3）
设抛物线的解析式为：y=ax2+bx+c
依题意有：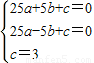
．
解之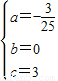
所以y=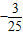
x2+3
（2）y=1，路灯的位置为（
，1）或（-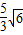
，1）．（只要写一个即可）
（3）当x=4时，y=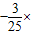
42+3=1.08，点到地面的距离为1.08+2=3.08
因为3.08-0.5=2.58＞2.5，所以能通过．
点评：由于抛物线在坐标系里这种特殊位置，还可以选择抛物线解析式的其他形式：
（1）对称轴是y轴，可以直接设y=ax2+c（缺一次项）；
（2）已知顶点，可以设抛物线顶点式；
（3）已知抛物线与x轴的两个交点，可以设抛物线交点式．
解答：
解：（1）如图，若以EF所在直线为x轴，经过H且垂直于EF的直线为y轴，建立平面直角坐标系，则E（-5，0），F（5，0），H（0，3）
设抛物线的解析式为：y=ax2+bx+c
依题意有：
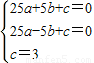．解之
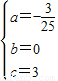
所以y=
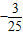x2+3（2）y=1，路灯的位置为（
，1）或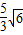（-，1）．（只要写一个即可）（3）当x=4时，y=
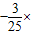42+3=1.08，点到地面的距离为1.08+2=3.08因为3.08-0.5=2.58＞2.5，所以能通过．
点评：由于抛物线在坐标系里这种特殊位置，还可以选择抛物线解析式的其他形式：
（1）对称轴是y轴，可以直接设y=ax2+c（缺一次项）；
（2）已知顶点，可以设抛物线顶点式；
（3）已知抛物线与x轴的两个交点，可以设抛物线交点式．
练习册系列答案
相关题目
