题目内容
如图,边长为2的正方形ABCD的对角线交于点O,把边BA、CD分别绕点B、C同时逆时针旋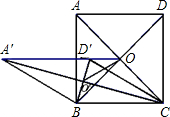 转60°得四边形A′BCD′,其对角线交点为O′,连接OD′.下列结论:
转60°得四边形A′BCD′,其对角线交点为O′,连接OD′.下列结论:
①四边形A′BCD′为菱形;
②S四边形A′BCD′=
S正方形ABCD;
③线段OD′的长为
-1;
④点O运动到点O′的路径是线段OO′.其中正确的结论共有( )
 转60°得四边形A′BCD′,其对角线交点为O′,连接OD′.下列结论:
转60°得四边形A′BCD′,其对角线交点为O′,连接OD′.下列结论:①四边形A′BCD′为菱形;
②S四边形A′BCD′=
| 1 |
| 2 |
③线段OD′的长为
| 3 |
④点O运动到点O′的路径是线段OO′.其中正确的结论共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:①根据旋转角是60°以及正方形的四个角都是直角可得∠BCD′=30°,然后证明A′B∥CD′,进而得到四边形A′BCD′是平行四边形,再根据A′B=BC,即可证明四边形A′BCD′是菱形;
②根据旋转角是60°求出点B到A′D′的距离是A′B的一半,也就是AB的一半,然后根据正方形的面积公式以及菱形的面积即可证明;
③先求出OA′的长度,再根据菱形的对边相等,减去正方形的边长即可;
④根据旋转的性质,点O以BC的中点为圆心,以BC的一半为半径逆时针旋转可以得到点O′,所以路径是弧而非线段.
②根据旋转角是60°求出点B到A′D′的距离是A′B的一半,也就是AB的一半,然后根据正方形的面积公式以及菱形的面积即可证明;
③先求出OA′的长度,再根据菱形的对边相等,减去正方形的边长即可;
④根据旋转的性质,点O以BC的中点为圆心,以BC的一半为半径逆时针旋转可以得到点O′,所以路径是弧而非线段.
解答:解:①根据题意,∠A′BA=∠D′CD=60°,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠BCD′=30°,
∴∠A′BC+∠BCD′=60°+90°+30°=180°,
∴A′B∥CD′,
又∵A′B=CD′=AB,
∴四边形A′BCD′是平行四边形,
∵AB=BC(正方形的边长相等),
∴四边形A′BCD′是菱形,故本题小题正确;
②∵∠ABA′=60°,AB=2,
∴点B到A′D′的距离是:
A′B=
AB=1,
∴S四边形A′BCD=BC•(
A′B)=2×1=2,
S正方形ABCD=BC•AB=2×2=4,
∴S四边形A′BCD=
S正方形ABCD,故本小题正确;
③∵点O是AC的中点,
∴OA′=A′B•sin60°+
BC=2×
+
×2=
+1,
∴OD′=OA′-A′D′=
+1-2=
-1,故本小题正确;
④根据菱形的对角线互相垂直可得△BCO′是直角三角形,
∴以BC的中点为圆心,以BC的一半为半径,点O逆时针旋转可以到达点O′的位置,经过路径是弧而不是线段OO′,故本小题错误.
综上所述,正确的结论有①②③共3个.
故选C.
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠BCD′=30°,
∴∠A′BC+∠BCD′=60°+90°+30°=180°,
∴A′B∥CD′,
又∵A′B=CD′=AB,
∴四边形A′BCD′是平行四边形,
∵AB=BC(正方形的边长相等),
∴四边形A′BCD′是菱形,故本题小题正确;
②∵∠ABA′=60°,AB=2,
∴点B到A′D′的距离是:
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形A′BCD=BC•(
| 1 |
| 2 |
S正方形ABCD=BC•AB=2×2=4,
∴S四边形A′BCD=
| 1 |
| 2 |
③∵点O是AC的中点,
∴OA′=A′B•sin60°+
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴OD′=OA′-A′D′=
| 3 |
| 3 |
④根据菱形的对角线互相垂直可得△BCO′是直角三角形,
∴以BC的中点为圆心,以BC的一半为半径,点O逆时针旋转可以到达点O′的位置,经过路径是弧而不是线段OO′,故本小题错误.
综上所述,正确的结论有①②③共3个.
故选C.
点评:本题考查了正方形的性质,菱形的判定与性质,直角三角形30°角所对的直角边等于斜边的性质,直角三角形斜边上的中线等于斜边的一半的性质,旋转变换,是综合题目,但难度不大,仔细分析即可求解.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目

 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
