题目内容
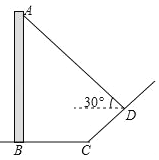
【题目】(2016山东潍坊第22题)如图，直立于地面上的电线杆AB，在阳光下落在水平地面和坡面上的影子分别是BC、CD，测得BC=6米，CD=4米，∠BCD=150°，在D处测得电线杆顶端A的仰角为30°，试求电线杆的高度（结果保留根号）
【答案】（2
+4）米．
【解析】
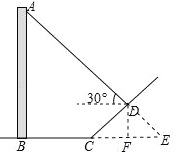
试题分析：延长AD交BC的延长线于E，作DF⊥BE于F，根据直角三角形的性质和勾股定理求出DF、CF的长，根据正切的定义求出EF，得到BE的长，根据正切的定义解答即可．
试题解析：延长AD交BC的延长线于E，作DF⊥BE于F，
∵∠BCD=150°，
∴∠DCF=30°，又CD=4，
∴DF=2，CF=
=2
，
由题意得∠E=30°，
∴EF=
=2，
∴BE=BC+CF+EF=6+4，
∴AB=BE×tanE=（6+4）×
=（2+4）米，
答：电线杆的高度为（2+4）米．
练习册系列答案
相关题目
