题目内容
某游泳池有水4000m3，先放水清洗池子．同时，工作人员记录放水的时间x（单位：分钟）与池内水量y（单位：m3） 的对应变化的情况，如下表：
（1）根据上表提供的信息，当放水到第80分钟时，池内有水多少m3？
（2）请你用函数解析式表示y与x的关系，并写出自变量x的取值范围．
| 时间x（分钟） | … | 10 | 20 | 30 | 40 | … |
| 水量y（m3） | … | 3750 | 3500 | 3250 | 3000 | … |
（2）请你用函数解析式表示y与x的关系，并写出自变量x的取值范围．
解：（1）由图表可知，每10分钟放水250m3，
∴第80分钟时，池内有水4000﹣8×250=2000m3。
（2）设函数关系式为y=kx+b，
∵x=20时，y=3500；x=40时，y=3000，
∴
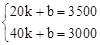，解得
，
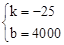∴y=﹣25x +4000。
将（10，3750），（30，3250）代入，适合。
∴函数关系式为y=﹣250 x +4000（0≤x≤160）
∴第80分钟时，池内有水4000﹣8×250=2000m3。
（2）设函数关系式为y=kx+b，
∵x=20时，y=3500；x=40时，y=3000，
∴
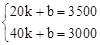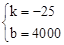，解得，∴y=﹣25x +4000。
将（10，3750），（30，3250）代入，适合。
∴函数关系式为y=﹣250 x +4000（0≤x≤160）
试题分析：（1）观察不难发现，每10分钟放水250m3，然后根据此规律求解即可。
（2）设函数关系式为y=kx+b，然后取两组数，利用待定系数法一次函数解析式求解即可。
练习册系列答案
阅读快车系列答案
相关题目
．动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于x轴，与折线A→D→C相交于点M，当P，Q两点中有一点到达终点时，另一点也随之停止运动．设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．
（k2≠0）的图象在第一象限的交点为C，过点C作x轴的垂线，垂足为D，若OA=OB=OD=2．
