题目内容
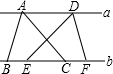 如图,a∥b,若要△ABC的面积=△DEF的面积相等,需增加条件
如图,a∥b,若要△ABC的面积=△DEF的面积相等,需增加条件
- A.AB=DE
- B.AC=DF
- C.BC=EF
- D.BE=AD
C
分析:过A作AZ⊥BC于Z,过D作DN⊥BC于N,推出AZ∥DN,得出四边形AZND是平行四边形,推出AZ=DN,根据三角形的面积得出△ABC的面积是 ×BC×AZ,△DEF的面积是
×BC×AZ,△DEF的面积是 ×EF×DN,即可得出答案.
×EF×DN,即可得出答案.
解答: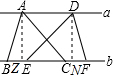
过A作AZ⊥BC于Z,过D作DN⊥BC于N,
则AZ∥DN,
∵a∥b,
∴四边形AZND是平行四边形,
∴AZ=DN,
∵△ABC的面积是 ×BC×AZ,△DEF的面积是
×BC×AZ,△DEF的面积是 ×EF×DN,
×EF×DN,
∴要使△ABC的面积=△DEF的面积相等,需增加条件是BC=EF,
故选C.
点评:本题考查了平行线间的距离,平行四边形的性质和判定,三角形的面积等知识点,题目比较典型,是一道比较好的题目.
分析:过A作AZ⊥BC于Z,过D作DN⊥BC于N,推出AZ∥DN,得出四边形AZND是平行四边形,推出AZ=DN,根据三角形的面积得出△ABC的面积是
 ×BC×AZ,△DEF的面积是
×BC×AZ,△DEF的面积是 ×EF×DN,即可得出答案.
×EF×DN,即可得出答案.解答:

过A作AZ⊥BC于Z,过D作DN⊥BC于N,
则AZ∥DN,
∵a∥b,
∴四边形AZND是平行四边形,
∴AZ=DN,
∵△ABC的面积是
 ×BC×AZ,△DEF的面积是
×BC×AZ,△DEF的面积是 ×EF×DN,
×EF×DN,∴要使△ABC的面积=△DEF的面积相等,需增加条件是BC=EF,
故选C.
点评:本题考查了平行线间的距离,平行四边形的性质和判定,三角形的面积等知识点,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
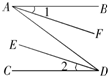 18、如图,AB∥CD,若要使∠1=∠2成立,则需添加的一个条件是
18、如图,AB∥CD,若要使∠1=∠2成立,则需添加的一个条件是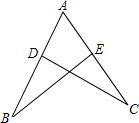 如图,AB=AC,若要使△ABE≌△ACD,根据SAS,则还需要
如图,AB=AC,若要使△ABE≌△ACD,根据SAS,则还需要 如图,AB∥CD,若要使∠1=∠2成立,则还需添加其他条件.
如图,AB∥CD,若要使∠1=∠2成立,则还需添加其他条件. 如图,a∥b,若要△ABC的面积=△DEF的面积相等,需增加条件( )
如图,a∥b,若要△ABC的面积=△DEF的面积相等,需增加条件( )