题目内容
 (2013•黔西南州)如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0,其中错误的有( )
(2013•黔西南州)如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0,其中错误的有( )分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:(1)图象与x轴有2个交点,依据根的判别式可知b2-4ac>0,正确;
(2)图象与y轴的交点在1的下方,所以c<1,错误;
(3)∵对称轴在-1的右边,∴-
>-1,又a<0,∴2a-b<0,正确;
(4)当x=1时,y=a+b+c<0,正确;
故错误的有1个.
故选:A.
(2)图象与y轴的交点在1的下方,所以c<1,错误;
(3)∵对称轴在-1的右边,∴-
| b |
| 2a |
(4)当x=1时,y=a+b+c<0,正确;
故错误的有1个.
故选:A.
点评:本题主要考查二次函数图象与系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
相关题目
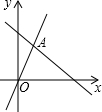 (2013•黔西南州)如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
(2013•黔西南州)如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )