题目内容
一轮船以16海里/时的速度从港口A出发向南偏东45°方向航行，另一轮船同时从港口A出发，以12海里/时的速度向北偏东45°方向航行，离开港口2个小时后，两船相距________海里．
40
分析：根据题意画出图形，判断出三角形的形状解答即可．
解答：
解：如图所示：∠1=∠2=45°，AB=12×2=24海里，AC=16×2=32海里，
∴∠BAC=∠1+∠2=90°，即△ABC是直角三角形，
∴BC=
=
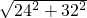=40海里．
点评：本题考查勾股定理在实际生活中的运用，解答此题的关键是根据题意画出图形，再根据勾股定理解答，体现了数形结合的优点．
分析：根据题意画出图形，判断出三角形的形状解答即可．
解答：
解：如图所示：∠1=∠2=45°，AB=12×2=24海里，AC=16×2=32海里，∴∠BAC=∠1+∠2=90°，即△ABC是直角三角形，
∴BC=
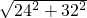==40海里．点评：本题考查勾股定理在实际生活中的运用，解答此题的关键是根据题意画出图形，再根据勾股定理解答，体现了数形结合的优点．
练习册系列答案
相关题目
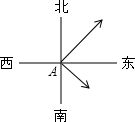已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（ ）| A、25海里 | B、30海里 | C、35海里 | D、40海里 |
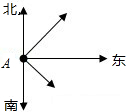已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距