题目内容
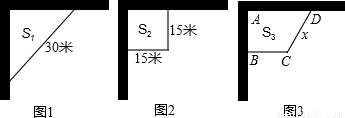
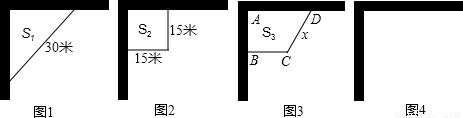
小明家打算建一个苗圃,苗圃的两边靠墙(这两堵墙互相垂直),另外的部分用30米长的篱笆围成.小明的爸爸提出一个问题:怎样围才能使苗圃的面积尽可能地大?小明思考后,设计了以下三种方案:方案一:围成斜边为30米的等腰直角三角形(如图1);
方案二:围成边长为15米的正方形(如图2);
方案三:围成直角梯形,其中∠BCD=120°(如图3).
解答下列问题:
(1)分别计算方案一、方案二中苗圃的面积S1,S2,并比较S1,S2的大小;
(2)设方案三中CD的长为x米,苗圃的面积为S3平方米,求S3与x之间的函数关系式,并求出S3的最大值;
(3)请你设计一种方案,使围成的苗圃面积比上述三个方案中的任何一个面积都大.(要求在图4中画出草图,标上必要的数据,并通过计算加以说明)

分析:(1)由三角形和正方形的面积公式求得S1、S2的大小;
(2)根据直角梯形面积公式列出函数关系式并求得最大值;
(3)若所围面积最大,则应该围成扇形,并计算证明之.
(2)根据直角梯形面积公式列出函数关系式并求得最大值;
(3)若所围面积最大,则应该围成扇形,并计算证明之.
解答: 解:(1)S1=
解:(1)S1=
×(30sin45°)2=225 m2,
S2=15×15=225 m2.
(2)S3=
×(30-x+30-x+
x)×x×sin60°
=15
x-
x2
=-
(x-20)2+150
∴当x=20时,S3取得最大值,为150
.
(3)我的方案是围成一扇形,则计算面积如下:
l=
×R=30,R=
S=
lR=
×30×
=
比较得知,S、S1、S2、S3中,S最大.
 解:(1)S1=
解:(1)S1=| 1 |
| 2 |
S2=15×15=225 m2.
(2)S3=
| 1 |
| 2 |
| 1 |
| 2 |
=15
| 3 |
3
| ||
| 8 |
=-
3
| ||
| 8 |
| 3 |
∴当x=20时,S3取得最大值,为150
| 3 |
(3)我的方案是围成一扇形,则计算面积如下:
l=
| π |
| 2 |
| 60 |
| π |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 60 |
| π |
| 900 |
| π |
比较得知,S、S1、S2、S3中,S最大.
点评:本题考查了同学们应用二次函数解决实际问题的能力.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

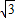 取1.74,π取3.15)
取1.74,π取3.15)