题目内容
校园内有一个高大的树，在实践活动课上，准备了如下测量工具“皮尺”、“高为1米的测角器”、“长为2米的标杆”来测量树的高度，请你设计测量方案并回答下列问题．（1）在你的设计方案中，选用的测量工具是
（2）在如图中画出你的测量方案示意图；
（3）你需要测量示意图中的哪些数据，并用a，b，c，αβ等字母表示测量的数据
（4）写出求树高的算式．
分析：（1）根据物理光学原理构造相似三角形，然后测量出两个三角形三条边的长度，故选择镜子和皮尺；
（2）根据相似三角形的性质，及题意所给条件，即可灵活设计方案；
（3）可借助相似三角形的对应边成比例的性质进行设计测量方法，先测得CE，EA与CD的大小；
（4）根据相似三角形的性质，可得：
=
，即AB=
．
（2）根据相似三角形的性质，及题意所给条件，即可灵活设计方案；
（3）可借助相似三角形的对应边成比例的性质进行设计测量方法，先测得CE，EA与CD的大小；
（4）根据相似三角形的性质，可得：
| CE |
| EA |
| DC |
| AB |
| ac |
| b |
解答：解：（1）镜子，皮尺；
（2）测量方案示意图；
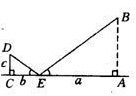
（3）EA（镜子离树的距离）=a，EC（人离镜子的距离）=b，DC（目高）=c；
（4）根据相似三角形的性质；可得：
=
；即AB=
．
故答案为：镜子，皮尺；EA（镜子离树的距离）=a，EC（人离镜子的距离）=b，DC（目高）=c．
（2）测量方案示意图；
（3）EA（镜子离树的距离）=a，EC（人离镜子的距离）=b，DC（目高）=c；
（4）根据相似三角形的性质；可得：
| CE |
| EA |
| DC |
| AB |
| ac |
| b |
故答案为：镜子，皮尺；EA（镜子离树的距离）=a，EC（人离镜子的距离）=b，DC（目高）=c．
点评：本题考查了解直角三角形的应用中的俯角仰角问题，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
校园内有一个高大的树，在实践活动课上，准备了如下测量工具“皮尺”、“高为1米的测角器”、“长为2米的标杆”来测量树的高度，请你设计测量方案并回答下列问题．