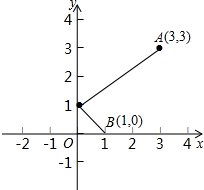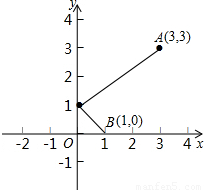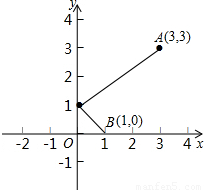题目内容
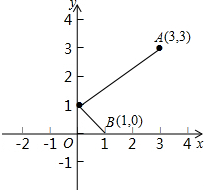 如图,一束光线从点A(3,3)出发,经Y轴上点c反射后正好经过点B(1,0),则点C在Y轴上的位置为
如图,一束光线从点A(3,3)出发,经Y轴上点c反射后正好经过点B(1,0),则点C在Y轴上的位置为分析:如下图,因为这束光线从点A(3,3)出发,经y轴上点C反射后正好经过点B(1,0),所以可设C(0,c),
由发射定律可知,∠1=∠OCB.延长AC交x轴于点D,则∠1=∠OCD.
所以∠OCB=∠OCD,从而可知OD=OB=1.
所以D(-1,0),设直线AD的解析式为y=kx+b,把A、D的坐标代入,即可求出它的解析式,就可求出该直线与y轴的交点C的坐标.
由发射定律可知,∠1=∠OCB.延长AC交x轴于点D,则∠1=∠OCD.
所以∠OCB=∠OCD,从而可知OD=OB=1.
所以D(-1,0),设直线AD的解析式为y=kx+b,把A、D的坐标代入,即可求出它的解析式,就可求出该直线与y轴的交点C的坐标.
解答: 解:∵这束光线从点A(3,3)出发,经y轴上点C反射后正好经过点B(1,0).
解:∵这束光线从点A(3,3)出发,经y轴上点C反射后正好经过点B(1,0).
∴设C(0,c),由反射定律可知,∠1=∠OCB,延长AC交x轴于点D,
则∠1=∠OCD.
∴∠OCB=∠OCD
∵CO⊥DB于O.则∠COD=∠BOC且OC=OC
∴Rt△OCD≌Rt△OCB
∴OD=OB=1,所以D(-1,0),
∴设直线AD的解析式为y=kx+b.则
∴
即直线AD的解析式为y=
x+
∴直线AD与y轴的交点C的坐标为(0,
).
 解:∵这束光线从点A(3,3)出发,经y轴上点C反射后正好经过点B(1,0).
解:∵这束光线从点A(3,3)出发,经y轴上点C反射后正好经过点B(1,0).∴设C(0,c),由反射定律可知,∠1=∠OCB,延长AC交x轴于点D,
则∠1=∠OCD.
∴∠OCB=∠OCD
∵CO⊥DB于O.则∠COD=∠BOC且OC=OC
∴Rt△OCD≌Rt△OCB
∴OD=OB=1,所以D(-1,0),
∴设直线AD的解析式为y=kx+b.则
|
∴
|
| 3 |
| 4 |
| 3 |
| 4 |
∴直线AD与y轴的交点C的坐标为(0,
| 3 |
| 4 |
点评:此类题目属于数形结合,结合轴对称分析出所需点的坐标,继而利用待定系数法求出直线解析式,最终解决问题.

练习册系列答案
相关题目
 13、如图,一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从点A到点B经过的路径长为
13、如图,一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从点A到点B经过的路径长为