Question

如图，将一张正方形纸片剪成四个小正方形，如图（1）；然后再将其中的一个正方形剪成四个小正方形，此时共有7个正方形，如图（2）；再将其中的一个正方形剪成四个小正方形，此时共有10个正方形，如图（3）．按此操作继续下去…



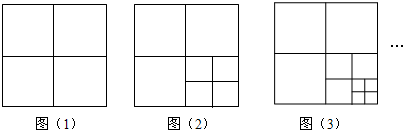
（1）根据以上操作方法，请你填写下表：

操作次数n	1	2	3	4	5	…．
正方形的个数S	4	7	10

（2）用代数式表示正方形的个数S和操作次数n之间的关系；
（3）按此方法操作下去，正方形的个数能否为2010个？若能，请说出是经过多少次操作后得到的；若不能，请说明理由．

Answer 1

（1）图1中正方形的个数为4=3×1+1；
图2中正方形的个数为7=3×2+1；
图3中正方形的个数为10=3×3+1；
…
可以发现：图几中正方形的个数等于3与几的乘积加1．
可得，图4、图5中正方形的个数分别为13、16．

操作次数n	1	2	3	4	5	…．
正方形的个数S	4	7	10	13	16

（2）设正方形的个数为S，操作次数为n，按照（1）中的规律可得：S=3n+1．

（3）设经过n次操作后，正方形的个数为2010个，则有3n+1=2010，
n=

2009

3

，
因为

2009

3

不是整数，所以不合题意，
所以按此方法操作下去，正方形的个数不能为2010个．