Question

【题目】定义：对角互补且有一组邻边相等的四边形称为奇异四边形．

（1）概念理解：

在平行四边形、菱形、矩形、正方形中，你认为属于奇异四边形的有__________ ；

（2）性质探究：

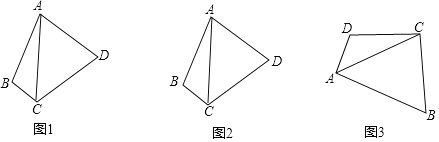
①如图1，四边形ABCD是奇异四边形，AB=AD，求证：CA平分∠BCD；

②如图2，四边形ABCD是奇异四边形，AB=AD，∠BCD=2α，试说明：cosα=；

（3）性质应用：

如图3，四边形ABCD是奇异四边形，四条边中仅有BC=CD，且四边形ABCD的周长为6+2，∠BAC=45°，AC=3，求奇异四边形ABCD的面积．

Answer 1

【答案】（1）正方形；（2）①见解析，②见解析；（3）9.

【解析】

（1）利用奇异四边形的定义直接判断即可；
（2）①如图1，过点A作AM⊥CB于M，AN⊥CD于N．证明△AMB≌△AND，根据全等三角形的性质得到AM=AN，根据角的内部到角两边距离相等的点在角平分线上即可证明.

②由①可知：∠ACD=∠BCD=α，根据CN=CD–DN=CD–BM=CD–（CM–BC）=CD–（CN–BC），得到CN=，在Rt△ACN中，根据余弦的定义即可证明.

（3）连接BD．由（2）可知：cos45°=，得到AD+AB=2AC×=6，根据四边形ABCD的周长为6+2，得到BC=CD=，得到∠DAB=90°，根据奇异四边形的性质，有∠BCD=90°，根据S四边形ABCD=S△ADB+S△BDC即可求解.

（1）根据奇异四边形的定义可知：正方形是奇异四边形，故答案为：正方形．

（2）①如图1，过点A作AM⊥CB于M，AN⊥CD于N．

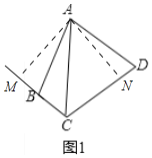
∵∠ABC+∠D=180°，∠ABM+∠ABC=180°，

∴∠ABM=∠D，

∵∠AMB=∠AND=90°，AB=AD，

∴△AMB≌△AND，

∴AM=AN，∵AM⊥CB于M，AN⊥CD于N，∴CA平分∠BCD．

②由①可知：∠ACD=∠BCD=α，

∵CN=CD–DN=CD–BM=CD–（CM–BC）=CD–（CN–BC），

∴CN=，

在Rt△ACN中，cosα==．

（3）如图3，连接BD．

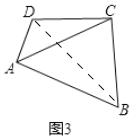
由（2）可知：cos45°=，∴AD+AB=2AC×=6，

∵四边形ABCD的周长为6+2，∴BC=CD=，

∵∠BAC=∠DAC=45°，

∴∠DAB=90°，

∵四边形是奇异四边形，∴∠BCD=90°，

∵AD+AB=6，∴（AD+AB）2=AD2+2ADAB+AB2=36，

∵AD2+AB2=BD2=BC2+CD2=20，

∴ADAB=8，∴S四边形ABCD=S△ADB+S△BDC=ADAB+CDBC=9．