题目内容
对于关于x的二次函数y=ax2-(2a-1)x-1(a≠0),下列说法正确的有( )
①无论a取何值,此二次函数图象与x轴必有两个交点; ②无论a取何值,图象必过两定点,且两定点之间的距离为
;
③当a>0时,函数在x<1时,y随x的增大而减小; ④当a<0时,函数图象截x轴所得的线段长度必大于2.
①无论a取何值,此二次函数图象与x轴必有两个交点; ②无论a取何值,图象必过两定点,且两定点之间的距离为
| 2 |
③当a>0时,函数在x<1时,y随x的增大而减小; ④当a<0时,函数图象截x轴所得的线段长度必大于2.
分析:①令y=0,即ax2-(2a-1)x-1=0,求出△,判断图象与x轴的交点个数,②把二次函数关系式y=ax2-(2a-1)x-1,可以判断两个定点,③求出对称轴,然后结合a的取值范围判断,④设函数图象与x轴的两交点为x1,x2,求出|x1-x2|进行判断.
解答:解:①令y=0,即ax2-(2a-1)x-1=0,△=4a2+1>0,即二次函数图象与x轴必有两个交点;故本选项正确,
②y=ax2-(2a-1)x-1=a(x-1)2+(x-1)-a,当x=2时,y=1,当x=0时,y=-1,图象必过两定点(2,1),(0,-1),两点之间的距离为2
,故本选项错误,
③二次函数y=ax2-(2a-1)x-1(a≠0)的对称轴为x=2-
,当a>0时不能判断y随x的增大而减小,故本选项错误;
④设函数图象与x轴的两交点为x1,x2,|x1-x2|=
=
>2,故函数图象截x轴所得的线段长度必大于2,故本选项正确,
故正确的有①④,
故选B.
②y=ax2-(2a-1)x-1=a(x-1)2+(x-1)-a,当x=2时,y=1,当x=0时,y=-1,图象必过两定点(2,1),(0,-1),两点之间的距离为2
| 2 |
③二次函数y=ax2-(2a-1)x-1(a≠0)的对称轴为x=2-
| 1 |
| a |
④设函数图象与x轴的两交点为x1,x2,|x1-x2|=
| (x1+x2)2-4x1x2 |
4+
|
故正确的有①④,
故选B.
点评:本题考查了抛物线与x轴的交点,要熟悉抛物线的对称性及抛物线与x轴的交点坐标.

练习册系列答案
相关题目
 ;
;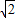 ;
;