题目内容
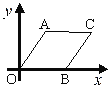
【题目】为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该电子产品的生产成本为每件40元,公司每月要支付其他费用15万元.该产品每月的销售量y(万件)与销售单价x(元)满足如图所示的一次函数关系:
(1)求每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)当销售单价定为多少元时,该公司每月销售利润最大.
(3)若相关部门要求该电子产品的销售单价不得低于其生产成本,且销售每件产品的利润率不能超过25%,则该公司最早用几个月可以还清无息贷款?

【答案】(1) y=-![]() x+8;(2) 60元;(3)6.
x+8;(2) 60元;(3)6.
【解析】
(1)根据题目中所给的图象,确定一次函数图象经过点(60,2)和(70,1),再利用待定系数法求每月销售量y(万件)与销售单价x(元)之间的函数关系式即可;(2)设当销售单价定为x元时,该公司每月销售利润为W万元,根据“总利润=单件的利润×销售量”列出W与x的二次函数关系式,再利用二次函数的性质求解即可;(3)根据题意求得x的取值范围,再求得在这一取值范围内w的最大值,再计算解答即可.
解:(1)设每月销售量y与x的函数解析式为y=kx+b(k≠0),把(60,2)和(70,1)代入得![]() 解得
解得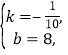 故y=-
故y=-![]() x+8.
x+8.
(2)设当销售单价定为x元时,该公司每月销售利润为W万元,则W=(x-40)![]() -15=-
-15=-![]() x2+12x-335=-
x2+12x-335=-![]() (x-60)2+25,则当销售单价定为60元时,该公司每月销售利润最大.
(x-60)2+25,则当销售单价定为60元时,该公司每月销售利润最大.
(3)由题意得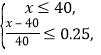 解得40≤x≤50,
解得40≤x≤50,
∵W=-![]() (x-60)2+25,∴抛物线开口向下,当x<60时,W随x的值增大而增大,∴当x=50时,每月有最大利润为W=-
(x-60)2+25,∴抛物线开口向下,当x<60时,W随x的值增大而增大,∴当x=50时,每月有最大利润为W=-![]() ×(50-60)2+25=15(万元),80÷15=
×(50-60)2+25=15(万元),80÷15=![]() =5
=5![]() ,∴该公司最早用6个月可以还清无息贷款.
,∴该公司最早用6个月可以还清无息贷款.