题目内容
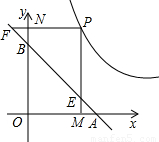
B题(油田考生做)如图,直线经过A(1,0),B(0,1)两点,点P是双曲线y=| 1 | 2x |
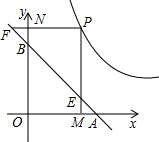 >0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.
>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.(1)求证:AF•BE=1;
(2)若平行于AB的直线与双曲线只有一个公共点,求公共点坐标.
分析:(1)本题可通过构建直角三角形来表示出AF,BE的长,过E,F分别作y轴,x轴的垂线,设垂足为D,C,那么△DBE和△FCA均为等腰直角三角形,因此AF=
FC,BE=
DE,而DE、FC正好是P点的横坐标和纵坐标,由此可得证.
(2)易知直线AB的解析式为y=-x+1,因此可设所求直线的解析式为y=-x+h,然后联立双曲线的解析式,由于两函数只有一个交点,因此得出的方程根的判别式的值为0,由此可求出直线的解析式进而可得出公共点的坐标.
| 2 |
| 2 |
(2)易知直线AB的解析式为y=-x+1,因此可设所求直线的解析式为y=-x+h,然后联立双曲线的解析式,由于两函数只有一个交点,因此得出的方程根的判别式的值为0,由此可求出直线的解析式进而可得出公共点的坐标.
解答:证明:(1)由直线经过A(1,0),B(0,1)两点,可得AB的解析式为y=-x+1,
过E作ED⊥y轴于D,过F作FC⊥x轴于C,则△FCA和△BDE均为等腰直角三角形.
∴AF=
FC,BE=
DE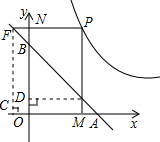
∴AF•BE=2•FC•DE
根据双曲线的解析式知:FC•DE=PM•PN=
∴AF•BE=1.
(2)易知:直线AB的解析式为y=-x+1,
因此设平行AB的直线l的解析式为y=-x+h,
设两函数唯一的公共点Q的坐标为(x,y),
则有:
,
即2x2-2hx+1=0,且△=4h2-8=0.
∴h=
(负值舍去),
∴x=
,y=
∴Q(
,
).
过E作ED⊥y轴于D,过F作FC⊥x轴于C,则△FCA和△BDE均为等腰直角三角形.
∴AF=
| 2 |
| 2 |

∴AF•BE=2•FC•DE
根据双曲线的解析式知:FC•DE=PM•PN=
| 1 |
| 2 |
∴AF•BE=1.
(2)易知:直线AB的解析式为y=-x+1,
因此设平行AB的直线l的解析式为y=-x+h,
设两函数唯一的公共点Q的坐标为(x,y),
则有:
|
即2x2-2hx+1=0,且△=4h2-8=0.
∴h=
| 2 |
∴x=
| ||
| 2 |
| ||
| 2 |
∴Q(
| ||
| 2 |
| ||
| 2 |
点评:本题考查了二次函数解析式的确定、函数图象交点以及二次函数和反比例函数的综合应用等知识及综合应用知识、解决问题的能力.

练习册系列答案
相关题目
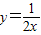 (x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.
(x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.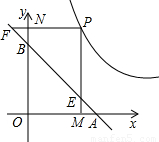
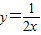 (x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.
(x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.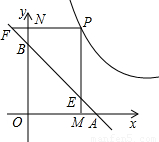
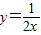 (x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.
(x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.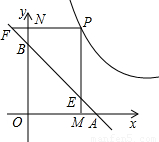
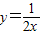 (x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.
(x>0)上任意一点,PM⊥x轴,PN⊥y轴,垂足分别为M、N,PM、PN的延长线与直线AB分别交于点E、F.