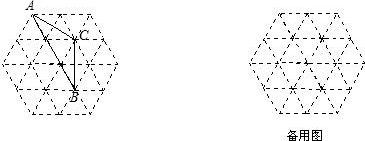Question

如图1-3是由边长为1的小正方形组成的网格，点A、B、C、D都在网格的格点上，AC、BD相交于点O．

（1）填空：如图1，当AB=2，连接AD．tan∠AOD=

3

；如图2，当AB=3，画AH⊥BD交BD的延长线于H点，则AH=

3 2

2

，tan∠AOD=

2

；如图3，当AB=4，tan∠AOD=

5

3

；
（2）猜想：当AB=n（n＞0）时，tan∠AOD=

n+1

n-1

；（结果用含有n的代数式表示）．请证明你的结论；
（3）如图4．两个正方形的一边CD、CG在同一直线上，连接CF、DE相交于点O，若tan∠COE=

19

6

．求正方形ABCD与正方形CEFG的边长之比．

Answer 1

分析：（1）设DCBE为正方形，连接CE，交BD于F，先由正方形的性质得出CF=DF=BF，BD⊥CE，再由AB∥DC，得△AOB∽△COD，根据相似三角形的对应边成比例得DO：BO=CD：AB，即可得OF：CF的值，然后在Rt△OCF中，求得tan∠COF的值，即为tan∠AOD的值；根据S_△ABD=

1

2

BD•AH=

1

2

AB•ED，即可求出AH；
（2）当AB=n（n＞0）时，tan∠AOD=

n+1

n-1

，同（1）证明即可；
（3）设正方形ABCD与正方形CEFG的边长之比为k，由（2）的结论得到

k+1

k-1

=

19

6

，解方程即可．

解答：解：（1）如图，设DCBE为正方形，连接CE，交BD于F．
∵四边形BCDE是正方形，
∴DF=CF=BF=

1

2

BD=

1

2

CE，BD⊥CE．
根据题意得：AB∥DC，
∴△AOB∽△COD，
∴DO：BO=CD：AB．
如图1，当AB=2时，DO：BO=CD：AB=1：2，
∴DO：DF=1：1.5=2：3，
∴OF：DF=1：3，即OF：CF=1：3．
在Rt△OCF中，tan∠COF=

CF

OF

=3，
∵∠AOD=∠COF，
∴tan∠AOD=3；
如图2，当AB=3时，
∵S_△ABD=

1

2

BD•AH=

1

2

AB•ED，
∴BD•AH=AB•ED，
∴AH=

AB•ED

BD

=

3×1

2

=

3 2

2

，
DO：BO=CD：AB=1：3，
∴DO：DF=1：2，
∴OF：DF=1：2，即OF：CF=1：2．
在Rt△OCF中，tan∠COF=

CF

OF

=2，
∵∠AOD=∠COF，
∴tan∠AOD=2；
如图3，当AB=4时，DO：BO=CD：AB=1：4，
∴DO：DF=1：2.5=2：5，
∴OF：DF=3：5，即OF：CF=3：5．
在Rt△OCF中，tan∠COF=

CF

OF

=

5

3

，
∵∠AOD=∠COF，
∴tan∠AOD=

5

3

；

（2）当AB=n（n＞0）时，tan∠AOD=

n+1

n-1

，理由如下：
设DCBE为正方形，连接CE，交BD于F．
∵四边形BCDE是正方形，
∴DF=CF=BF=

1

2

BD=

1

2

CE，BD⊥CE．
根据题意得：AB∥DC，
∴△AOB∽△COD，
∴DO：BO=CD：AB=1：n，
∴DO：DF=1：

n+1

2

=2：（n+1），
∴OF：DF=（n-1）：（n+1），即OF：CF=（n-1）：（n+1）．
在Rt△OCF中，tan∠COF=

CF

OF

=

n+1

n-1

，
∵∠AOD=∠COF，
∴tan∠AOD=

n+1

n-1

；

（3）设正方形ABCD与正方形CEFG的边长之比为k，
则

k+1

k-1

=

19

6

，
解得：k=

25

13

．
故正方形ABCD与正方形CEFG的边长之比为

25

13

．
故答案为（1）3；

3 2

2

，2；

5

3

；
（2）

n+1

n-1

．

点评：此题考查了正方形的性质，相似三角形的判定与性质，三角函数的定义，三角形的面积．此题难度适中，解题的关键是准确作出辅助线，注意转化思想与数形结合思想的应用．