题目内容
根据题意,解答下列问题:
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长;
(2)公式推导:类比(1)的求解过程,P1(x1,y1),P2(x2,y2)是平面直角坐标系内的两点,如图2,请你通过构造直角三角形的方法推导公式P1P2=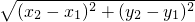 ;
;
(3)公式应用:已知:如图3,A(6,1),B(2,4),问:是否在x轴、y轴上分别存在P、Q两点,使得四边形ABQP的周长最短?若存在,求出四边形ABQP的周长;若不存在,请说明理由.

解:(1)∵直线y=2x+4与x轴、y轴分别交于A、B两点
∴A点坐标为(-2,0)B点坐标为(0,4)
∴AB的长为 ;
;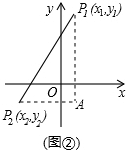
(2)如图过P1、P2分别作两轴的平行线,交于点A,
则P1A=x2-x1,P2A=y2-y1
∴P1P2=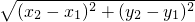 ;
;
(3)由(2)中得AB= =5
=5
设P、Q两点的坐标为(x,0),(0,y)
则AP= PQ=
PQ= BQ=
BQ=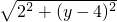
周长为AP+PQ+BQ+AB
要使周长最小,则AP+PQ+BQ应该最小
由公式x2+y2≥2xy,当且仅当x=y时满足
类推得x2+y2+z2≥xy+xz+yz当且仅当x=y=z时取等号
∴当AP=PQ=BQ时取得最小值
计算得最小值为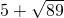 .
.
分析:根据勾股定理,知道两边的坐标求出两边的长,继而可以轻松求出第三边的长度.利用x+y≥ 得当两项相等时相加最小,类推出当AP=PQ=BQ时取得最小值,利用(2)中所得的公式可以求出.
得当两项相等时相加最小,类推出当AP=PQ=BQ时取得最小值,利用(2)中所得的公式可以求出.
点评:①求边长可以有很多种求法,其中利用直角三角形是常用的一种,勾股定理或三角函数等.
②合理利用不等式的关系求解.
∴A点坐标为(-2,0)B点坐标为(0,4)
∴AB的长为
 ;
;
(2)如图过P1、P2分别作两轴的平行线,交于点A,
则P1A=x2-x1,P2A=y2-y1
∴P1P2=
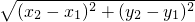 ;
;(3)由(2)中得AB=
 =5
=5设P、Q两点的坐标为(x,0),(0,y)
则AP=
 PQ=
PQ= BQ=
BQ=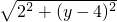
周长为AP+PQ+BQ+AB
要使周长最小,则AP+PQ+BQ应该最小
由公式x2+y2≥2xy,当且仅当x=y时满足
类推得x2+y2+z2≥xy+xz+yz当且仅当x=y=z时取等号
∴当AP=PQ=BQ时取得最小值
计算得最小值为
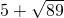 .
.分析:根据勾股定理,知道两边的坐标求出两边的长,继而可以轻松求出第三边的长度.利用x+y≥
 得当两项相等时相加最小,类推出当AP=PQ=BQ时取得最小值,利用(2)中所得的公式可以求出.
得当两项相等时相加最小,类推出当AP=PQ=BQ时取得最小值,利用(2)中所得的公式可以求出.点评:①求边长可以有很多种求法,其中利用直角三角形是常用的一种,勾股定理或三角函数等.
②合理利用不等式的关系求解.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 ;
;

