题目内容
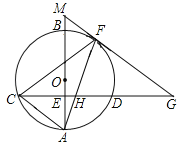
【题目】如图,AB是⊙O的直径,CD⊥AB,交⊙O于C、D两点,交AB点E、F是弧BD上一点,过点F作一条直线,交CD的延长线于点G,交AB的延长线于点M.连结AF,交CD于点H,GF=GH.
(1)求证:MG是⊙O的切线;
(2)若弧AF=弧CF,求证:HC=AC;
(3)在(2)的条件下,若tanG=![]() ,AE=6,求GM的值.
,AE=6,求GM的值.
【答案】(1)证明见解析;(2)证明见解析;(3)GM=![]() .
.
【解析】
(1)连接OF,先证明∠GFH=∠GHF=∠AHE,再证明OF⊥GM即可.
(2)证明AC∥GM,再证明∠CAH=∠CHA即可得到答案.
(3)解直角三角形求出EC,AC,设GF=GH=x,则CG=CH+GH=AC+GH=10+x,利用切线长定理构建方程求出x即可解决问题.
(1)证明:连接OF.
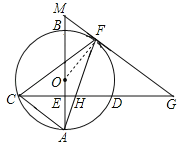
∴AB⊥CD,
∴∠AEH=90°,
∴∠EAH+∠AHE=90°,
∵GF=GH,
∴∠GFH=∠GHF=∠AHE,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠OFA+∠GFH=90°,
∴OF⊥GM,
∴MG是⊙O的切线.
(2)证明:∵弧AF=弧CF,
∴OF垂直平分线段AC
∵OF⊥MG,
∴AC∥GM,
∴∠CAH=∠GFH,
∵∠CHA=∠GHF,∠HGF=∠GFH,
∴∠CAH=∠CHA,
∴CA=CH.
(3)解:∵AC∥GM,
∴∠G=∠ACH,
∴tan∠CAH=tan∠G=![]() ,
,
∵AE=6,
∴EC=8,AC=![]() ,
,
设GF=GH=x,则CG=CH+GH=AC+GH=10+x,
∵CD=2EC=16,
∴GD=10+x﹣16=x﹣6,
∵GF2=GDGC,
∴x2=(x﹣6)(x+10),
解得x=15,
∴EG=CG﹣CE=25﹣8=17,
∵tan∠G=![]() ,
,
∴EM=![]() ,
,
∴GM=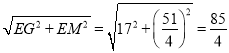 .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目