题目内容
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线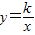 经过点B、E,若C′、D′在y轴上,则k= .
经过点B、E,若C′、D′在y轴上,则k= .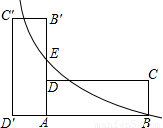
【答案】分析:根据矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,得到AD′=AD=2,D′C′=A′B′=AB=6,再根据E是AB′的中点,得到AE=3,利用若C′、D′在y轴上,设B点的坐标为(8,y),则E点的坐标为(2,y+3),代入反比例函数的解析式即可求得k值.
解答:解:∵矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,
∴AD′=AD=2,D′C′=A′B′=AB=6,
∵E是AB′的中点,
∴AE=3,
∵若C′、D′在y轴上,
∴设B点的坐标为(8,y),则E点的坐标为(2,y+3),
∵若双曲线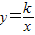 经过点B、E,
经过点B、E,
∴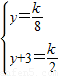
解得: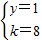
故答案为:8.
点评:本题考查了反比例函数的综合题,根据题目中提供的条件设出点D和点E的坐标是解决此题的关键.
解答:解:∵矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,
∴AD′=AD=2,D′C′=A′B′=AB=6,
∵E是AB′的中点,
∴AE=3,
∵若C′、D′在y轴上,
∴设B点的坐标为(8,y),则E点的坐标为(2,y+3),
∵若双曲线
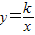 经过点B、E,
经过点B、E,∴
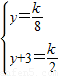
解得:
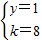
故答案为:8.
点评:本题考查了反比例函数的综合题,根据题目中提供的条件设出点D和点E的坐标是解决此题的关键.

练习册系列答案
相关题目
 度不考虑)
度不考虑)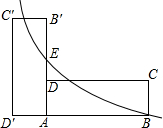 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线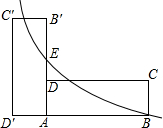 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线 经过点B、E,若C′、D′在y轴上,则k=________.
经过点B、E,若C′、D′在y轴上,则k=________.