题目内容
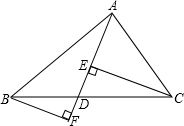 如图,已知:CE⊥AD于E,BF⊥AD于F,你能说明△BDF和△CDE全等吗?若能,请你说明理由;若不能,在不用增加辅助线的情况下,请添加其中一个适当的条件,这个条件是________,来说明这两个三角形全等,并写出证明过程.
如图,已知:CE⊥AD于E,BF⊥AD于F,你能说明△BDF和△CDE全等吗?若能,请你说明理由;若不能,在不用增加辅助线的情况下,请添加其中一个适当的条件,这个条件是________,来说明这两个三角形全等,并写出证明过程.
BD=DC或DF=DE或BF=CE
分析:根据全等的条件可知,只有“CE⊥AD于E,BF⊥AD于F”不能说明△BDF和△CDE全等,若要全等,需添一条边对应相等,所以添加的条件是BD=DC或DF=DE或BF=CE.
解答:①不能;
②添加的条件是BD=DC或DF=DE或BF=CE;
③证明:
∵CE⊥AD于E,BF⊥AD于F,
∴∠BFD=∠CED,
∵∠BDF=∠CDE,BD=DC,
∴△BDF≌△CDE.
点评:本题考查三角形全等的判定,判定两个三角形全等的一般方法有:SSS、SAS、AAS、HL.
判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
分析:根据全等的条件可知,只有“CE⊥AD于E,BF⊥AD于F”不能说明△BDF和△CDE全等,若要全等,需添一条边对应相等,所以添加的条件是BD=DC或DF=DE或BF=CE.
解答:①不能;
②添加的条件是BD=DC或DF=DE或BF=CE;
③证明:
∵CE⊥AD于E,BF⊥AD于F,
∴∠BFD=∠CED,
∵∠BDF=∠CDE,BD=DC,
∴△BDF≌△CDE.
点评:本题考查三角形全等的判定,判定两个三角形全等的一般方法有:SSS、SAS、AAS、HL.
判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
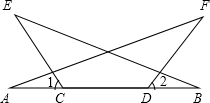 如图,已知:CE=DF,AC=BD,∠1=∠2,求证:∠A=∠B.
如图,已知:CE=DF,AC=BD,∠1=∠2,求证:∠A=∠B.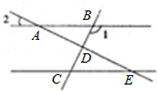 如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的( )
如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的( ) 如图,已知AB∥CE,DB平分∠ADC,AE∥BD,∠C=2∠E,求证:四边形ABCD是等腰梯形.
如图,已知AB∥CE,DB平分∠ADC,AE∥BD,∠C=2∠E,求证:四边形ABCD是等腰梯形. 如图,已知:CE⊥AD于E,BF⊥AD于F.在不用增加辅助线的情况下,请添加其中一个适当的条件,使△BDF和△CDE全等这个条件是
如图,已知:CE⊥AD于E,BF⊥AD于F.在不用增加辅助线的情况下,请添加其中一个适当的条件,使△BDF和△CDE全等这个条件是 如图,已知BD∥CE.
如图,已知BD∥CE.