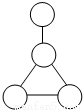
题目内容
黑、红、黄三种颜色涂在如图所示的圆圈中，每个圆圈只能涂一种颜色，并且要使每条连线两端的圆圈上涂上不同的颜色，则共有多少种不同涂法？
解：如图所示：
故要使每条连线两端的圆圈上涂上不同的颜色，则共有12种不同涂法．
分析：根据已知列出树状图，进而得出所有的符合要求的结果即可．
点评：此题主要考查了列表法或树状图法求概率的知识．此题比较简单，注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．
故要使每条连线两端的圆圈上涂上不同的颜色，则共有12种不同涂法．
分析：根据已知列出树状图，进而得出所有的符合要求的结果即可．
点评：此题主要考查了列表法或树状图法求概率的知识．此题比较简单，注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．
练习册系列答案
名校课堂系列答案
相关题目
下列游戏对双方公平的是（ ）
| A、随意转动被等分成3个扇形，且分别均匀涂有红、黄、绿三种颜色的转盘，若指针指向绿色区域，则小明胜，否则小亮胜 | B、从一个装有3个红球，2个黄球和2个黑球（这些球除颜色外完全相同）的袋中任意摸出一个球，若是红球，则小明胜，否则小亮胜 | C、投掷一枚均匀的正方体形状的骰子，若偶数点朝上，则小明胜，若是奇数点朝上，则小亮胜 | D、从分别标有数1，2，3，4，5的五张纸条中，任意抽取一张，若抽到的纸条所标的数字为偶数，则小明胜，若抽到的纸条所标的数字为奇数，则小亮胜 |
黑、红、黄三种颜色涂在如图所示的圆圈中，每个圆圈只能涂一种颜色，并且要使每条连线两端的圆圈上涂上不同的颜色，则共有多少种不同涂法？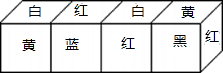
在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色，现有涂色方式完全相同的四个正方体，如图拼成一个长方体，请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色．