题目内容
 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是
- A.弦AB的长等于圆内接正六边形的边长
- B.弦AC的长等于圆内接正十二边形的边长
- C.
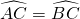
- D.∠BAC=30°
D
分析:根据正多边形的性质和圆的相关概念对四个选项逐一进行分析.
解答:A、因为OA=OB,OA=AB,所以OA=OB=AB,所以△ABO为等边三角形,∠AOB=60°,以AB为一边可构成
正六边形,故正确;
B、因为OC⊥AB,根据垂径定理可知, =
= ;再根据A中结论,弦AC的长等于圆内接正十二边形的边长,故正确;
;再根据A中结论,弦AC的长等于圆内接正十二边形的边长,故正确;
C、根据垂径定理, =
= ,故正确;
,故正确;
D、根据圆周角定理,圆周角的度数等于它所对的圆心角的度数的一半,∠BAC= ∠BOC=
∠BOC= ×
× ∠BOA=
∠BOA= ×60°=15°,故错误.
×60°=15°,故错误.
故选D.
点评:此题主要考查正多边形和圆的计算问题,属于常规题,要注意圆周角定理的应用.
分析:根据正多边形的性质和圆的相关概念对四个选项逐一进行分析.
解答:A、因为OA=OB,OA=AB,所以OA=OB=AB,所以△ABO为等边三角形,∠AOB=60°,以AB为一边可构成
正六边形,故正确;
B、因为OC⊥AB,根据垂径定理可知,
 =
= ;再根据A中结论,弦AC的长等于圆内接正十二边形的边长,故正确;
;再根据A中结论,弦AC的长等于圆内接正十二边形的边长,故正确;C、根据垂径定理,
 =
= ,故正确;
,故正确;D、根据圆周角定理,圆周角的度数等于它所对的圆心角的度数的一半,∠BAC=
 ∠BOC=
∠BOC= ×
× ∠BOA=
∠BOA= ×60°=15°,故错误.
×60°=15°,故错误.故选D.
点评:此题主要考查正多边形和圆的计算问题,属于常规题,要注意圆周角定理的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
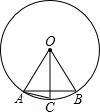 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )| A、弦AB的长等于圆内接正六边形的边长 | ||||
| B、弦AC的长等于圆内接正十二边形的边长 | ||||
C、
| ||||
| D、∠BAC=30° |

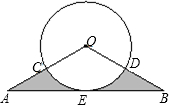 如图,在△OAB中,OA=OB=2,∠OAE=30°,⊙O切AB于E,且分别交OA、OB于C、D,求图中阴影部分的面积.
如图,在△OAB中,OA=OB=2,∠OAE=30°,⊙O切AB于E,且分别交OA、OB于C、D,求图中阴影部分的面积. 7、如图,在⊙O中,OA∥BC,∠B=40°,则∠OAC的度数是( )
7、如图,在⊙O中,OA∥BC,∠B=40°,则∠OAC的度数是( )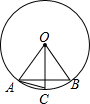 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的是( ) (2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=
(2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=