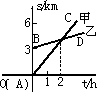题目内容
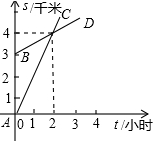
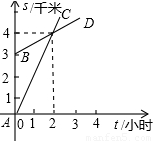
 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为
如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为分析:根据图分别求出甲乙两人行走时的路程与时间的关系一次函数,设s=kt+b,甲走的是C路线,乙走的是D路线,C、D线均过(2,4)点,且分别过(0,0),(0,3),很容易求得,要求他们三小时后的距离即是求当t=3时,sC与sD的差.
解答:解:由题,图可知甲走的是C路线,乙走的是D路线,
设s=kt+b①,
因为C过(0,0),(2,4)点,
所以代入①得:k=2,b=0,
所以sC=2t.
因为D过(2,4),(0,3)点,
代入①中得:k=
,b=3,
所以sD=
t+3,
当t=3时,sC-sD=6-
=
.
设s=kt+b①,
因为C过(0,0),(2,4)点,
所以代入①得:k=2,b=0,
所以sC=2t.
因为D过(2,4),(0,3)点,
代入①中得:k=
| 1 |
| 2 |
所以sD=
| 1 |
| 2 |
当t=3时,sC-sD=6-
| 9 |
| 2 |
| 3 |
| 2 |
点评:本题考查的是一元函数在实际生活中的应用,数形结合,求其解析式,可根据题意解出符合题意的解,中档题很常见的题型.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目