题目内容
解答题(1)已知C为线段AB的中点,D在线段CB上,且DA=6,DB=4,求CD的长度;

(2)一个角比它的余角的
| 1 | 2 |
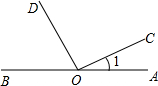
(3)如图,已知∠1=24°40′,OD平分∠BOC,求∠AOD的度数.
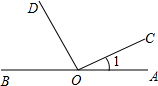
分析:(1)首先根据线段的和的关系求得总线段,再根据线段的中点的概念,求得BC,从而利用线段的差进一步求得CD;
(2)根据两个互为余角的关系由其中一个角表示另一个角,再根据题意列方程即可;
(3)首先根据邻补角求得∠BOC,再根据角平分线的概念求得∠COD,再利用角之间的求和方法计算∠AOD.
(2)根据两个互为余角的关系由其中一个角表示另一个角,再根据题意列方程即可;
(3)首先根据邻补角求得∠BOC,再根据角平分线的概念求得∠COD,再利用角之间的求和方法计算∠AOD.
解答:解:(1)∵DA=6,DB=4,
∴AB=DA+DB=6+4=10,
∵C为线段AB的中点,
∴CB=
AB=5,
∴CD=CB-DB=5-4=1;
(2)∠1的余角为90°-∠1,
由题意得∠1=
(90°-∠1)-15°,
∴∠1=20°;
(3)∵∠1=24°40′,
∴∠BOC=∠AOB-∠1=180°-24°40′=155°20′,
∵OD平分∠BOC,
∴∠COD=
∠BOC=77°40′,
∵∠AOD=∠COD+∠AOC,
∴∠AOD=77°40′+24°40′=102°20′.
故答案为1、20°、102°20′.
∴AB=DA+DB=6+4=10,
∵C为线段AB的中点,
∴CB=
| 1 |
| 2 |
∴CD=CB-DB=5-4=1;
(2)∠1的余角为90°-∠1,
由题意得∠1=
| 1 |
| 2 |
∴∠1=20°;
(3)∵∠1=24°40′,
∴∠BOC=∠AOB-∠1=180°-24°40′=155°20′,
∵OD平分∠BOC,
∴∠COD=
| 1 |
| 2 |
∵∠AOD=∠COD+∠AOC,
∴∠AOD=77°40′+24°40′=102°20′.
故答案为1、20°、102°20′.
点评:理解线段的中点的概念、角平分线的概念、余角的概念.能够结合图形找到线段、角之间的和或差的关系.

练习册系列答案
相关题目

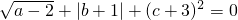 ,求方程ax2+bx+c=0的根.
,求方程ax2+bx+c=0的根.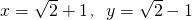 ,求
,求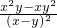 的值.
的值.
 还少15°,求这个角;
还少15°,求这个角;