题目内容
(2013•哈尔滨)已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.
(1)如图1,求证:∠EAF=∠ABD;
(2)如图2,当AB=AD时,M是线段AG上一点,连接BM,ED,MF,MF的延长线交ED于点N,∠MBF=
∠BAF,AF=
AD,试探究FM和FN之间的数量关系,并证明你的结论.
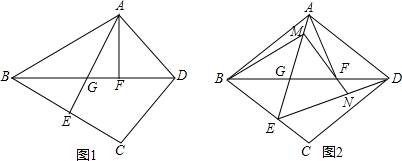
(1)如图1,求证:∠EAF=∠ABD;
(2)如图2,当AB=AD时,M是线段AG上一点,连接BM,ED,MF,MF的延长线交ED于点N,∠MBF=
| 1 |
| 2 |
| 2 |
| 3 |

分析:(1)如图1,连接FE、FC,构建全等三角形△ABF≌△CBF(SAS),则易证∠BAF=∠2,FA=FC;根据垂直平分线的性质、等量代换可知FE=FA,∠1=∠BAF,则∠5=∠6.然后由四边形内角和是360°、三角形内角和定理求得∠5+∠6=∠3+∠4,则∠5=∠4,即∠EAF=∠ABD;
(2)FM=
FN.理由如下:由△AFG∽△BFA,易得∠AGF=∠BAF,所以结合已知条件和图形得到∠MBG=∠BMG.易证△AGF∽△DGA,则对应边成比例:
=
=
.即
=
=
.
设GF=2a(a>0),AG=3a,则GD=
a,FD=
a;利用平行线(BE∥AD)截线段成比例易得
=
,则
=
=
.设EG=2k(k>0),所以BG=MG=3k.如图2,过点F作FQ∥ED交AE于点Q.则
=
=
=
,又由FQ∥ED,易证得
=
=
,所以FM=
FN.
(2)FM=
| 7 |
| 2 |
| GF |
| AG |
| AG |
| GD |
| AF |
| AD |
| GF |
| AG |
| AG |
| GD |
| 2 |
| 3 |
设GF=2a(a>0),AG=3a,则GD=
| 9 |
| 2 |
| 5 |
| 2 |
| BG |
| GD |
| EG |
| AG |
| EG |
| BG |
| AG |
| GD |
| 2 |
| 3 |
| GQ |
| QE |
| GF |
| FD |
| 2a | ||
|
| 4 |
| 5 |
| MF |
| FN |
| MQ |
| QE |
| 7 |
| 2 |
| 7 |
| 2 |
解答: (1)证明:如图1,连接FE、FC.
(1)证明:如图1,连接FE、FC.
∵点F在线段EC的垂直平分线上,
∴FE=FC,
∴∠1=∠2.
∵△ABD和△CBD关于直线BD对称(点A的对称点是点C),
∴AB=CB,∠4=∠3,
∵在△ABF与△CBF中,
,
∴△ABF≌△CBF(SAS),
∴∠BAF=∠2,FA=FC,
∴FE=FA,∠1=∠BAF,
∴∠5=∠6.
∵∠1+∠BEF=180°,
∴∠BAF+∠BEF=180°
∵∠BAF+∠BEF+∠AFE+∠ABE=360°,
∴∠AFE+∠ABE=180°.
又∵∠AFE+∠5+∠6=180°,
∴∠5+∠6=∠3+∠4,
∴∠5=∠4,即∠EAF=∠ABD;
(2)FM=
FN.理由如下:
如图2,由(1)知,∠EAF=∠ABD.
又∵∠AFB=∠GFA,
∴△AFG∽△BFA,
∴∠AGF=∠BAF.
又∵∠MBF=
∠BAF,
∴∠MBF=
∠AGF.
∵∠AGF=∠MBG+∠BMG,
∴∠MBG=∠BMG,
∴BG=MG.
∵AB=AD,
∴∠ADB=∠ABD=∠EAF.
又∵∠FGA=∠AGD,
∴△AGF∽△DGA,
∴
=
=
.
∵AF=
AD,
∴
=
=
.
设GF=2a(a>0),AG=3a,
∴GD=
a,
∴FD=
a
∵∠CBD=∠ABD,∠ABD=∠ADB,
∴∠CBD=∠ADB,
∴BE∥AD,
∴
=
,
∴
=
=
.
设EG=2k(k>0),
∴BG=MG=3k.
如图2,过点F作FQ∥ED交AE于点Q.则
=
=
=
,
∴GQ=
QE,
∴GQ=
EG=
k,MQ=3k+
k=
k.
∵FQ∥ED,
∴
=
=
,
∴FM=
FN.
 (1)证明:如图1,连接FE、FC.
(1)证明:如图1,连接FE、FC.∵点F在线段EC的垂直平分线上,
∴FE=FC,
∴∠1=∠2.
∵△ABD和△CBD关于直线BD对称(点A的对称点是点C),
∴AB=CB,∠4=∠3,
∵在△ABF与△CBF中,
|
∴△ABF≌△CBF(SAS),
∴∠BAF=∠2,FA=FC,
∴FE=FA,∠1=∠BAF,
∴∠5=∠6.
∵∠1+∠BEF=180°,
∴∠BAF+∠BEF=180°
∵∠BAF+∠BEF+∠AFE+∠ABE=360°,
∴∠AFE+∠ABE=180°.
又∵∠AFE+∠5+∠6=180°,
∴∠5+∠6=∠3+∠4,
∴∠5=∠4,即∠EAF=∠ABD;
(2)FM=
| 7 |
| 2 |
如图2,由(1)知,∠EAF=∠ABD.
又∵∠AFB=∠GFA,
∴△AFG∽△BFA,
∴∠AGF=∠BAF.
又∵∠MBF=
| 1 |
| 2 |
∴∠MBF=
| 1 |
| 2 |
∵∠AGF=∠MBG+∠BMG,
∴∠MBG=∠BMG,
∴BG=MG.
∵AB=AD,
∴∠ADB=∠ABD=∠EAF.
又∵∠FGA=∠AGD,
∴△AGF∽△DGA,
∴
| GF |
| AG |
| AG |
| GD |
| AF |
| AD |
∵AF=
| 2 |
| 3 |
∴
| GF |
| AG |
| AG |
| GD |
| 2 |
| 3 |
设GF=2a(a>0),AG=3a,
∴GD=
| 9 |
| 2 |
∴FD=
| 5 |
| 2 |
∵∠CBD=∠ABD,∠ABD=∠ADB,
∴∠CBD=∠ADB,
∴BE∥AD,
∴
| BG |
| GD |
| EG |
| AG |
∴
| EG |
| BG |
| AG |
| GD |
| 2 |
| 3 |
设EG=2k(k>0),
∴BG=MG=3k.
如图2,过点F作FQ∥ED交AE于点Q.则
| GQ |
| QE |
| GF |
| FD |
| 2a | ||
|
| 4 |
| 5 |
∴GQ=
| 4 |
| 5 |
∴GQ=
| 4 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 35 |
| 9 |
∵FQ∥ED,
∴
| MF |
| FN |
| MQ |
| QE |
| 7 |
| 2 |
∴FM=
| 7 |
| 2 |
点评:本题综合考查了相似三角形的判定与性质,平行线分线段成比例,三角形内角和定理以及四边形内角和是360度等知识点.难度较大,综合性较强.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目