Question

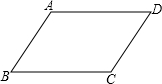
39、我们知道，平行四边形的对角相等，其证明过程如下，请在每一步括号内填写理由．
已知：如图，四边形ABCD是平行四边形．
求证：∠A=∠C，∠B=∠D．

Answer 1

分析：已知四边形ABCD是平行四边形，由平行四边形的性质可得AD∥BC，AB∥CD；再由内错角定理得∠A+∠B=180°，∠B+∠C=180°，再移项，由等式的传递性质，可得出∠A=∠C，同理可得∠B=∠D．

解答：证明：∵四边形ABCD是平行四边形（已知），
∴AD∥BC，AB∥CD（平行四边形的性质）．
∴∠A+∠B=180°，∠B+∠C=180°（内错角定理）．
∴∠A=180°-∠B，∠C=180°-∠B（加减法的移项）．
∴∠A=∠C（等号的传递性质）．
同理，可证∠B=∠D．

点评：本题主要考查了平行四边形的性质，并利用性质解题．平行四边形基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．