题目内容
⊙O1与⊙O2相交于A、B，公共弦AB=16，两圆半径分别为10、17，则圆心距O1O2=
21或9
21或9
．分析：利用连心线垂直平分公共弦的性质，构造直角三角形利用勾股定理及有关性质解题．
解答：
解：如图，∵⊙O1与⊙O2相交于A、B两点，
∴O1O2⊥AB，且AD=BD；
又∵AB=16，
∴AD=8，
∴在Rt△AO1D中，根据勾股定理知O1D=6；
在Rt△AO2D中，根据勾股定理知O2D=15，
∴O1O2=O1D+O2D=21；
同理知，当小圆圆心在大圆内时，解得O1O2=15-6=9．
故答案是：21或9．
解：如图，∵⊙O1与⊙O2相交于A、B两点，∴O1O2⊥AB，且AD=BD；
又∵AB=16，
∴AD=8，
∴在Rt△AO1D中，根据勾股定理知O1D=6；
在Rt△AO2D中，根据勾股定理知O2D=15，
∴O1O2=O1D+O2D=21；
同理知，当小圆圆心在大圆内时，解得O1O2=15-6=9．
故答案是：21或9．
点评：本题主要考查了圆与圆的位置关系，勾股定理等知识点．注意，解题时要分类讨论，以防漏解．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
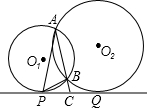如图，⊙O1与⊙O2相交于A，B两点，直线PQ与⊙O1相切于点P，与⊙O2相切于点Q，AB的延长线交PQ于C，连接PA，PB．下列结论：①PC=CQ；② |
| PB |
|
| BQ |
| A、3个 | B、2个 | C、1个 | D、0个 |
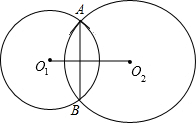如图，⊙O1与⊙O2相交于A、B．已知两圆的半径r1=10，r2=17，圆心距O1O2=21，公共弦AB等于（ ）A、2
| ||
| B、16 | ||
C、6
| ||
| D、17 |
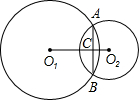已知：如图，⊙O1与⊙O2相交于A、B，若两圆半径分别为12和5，O1O2=13，则AB=